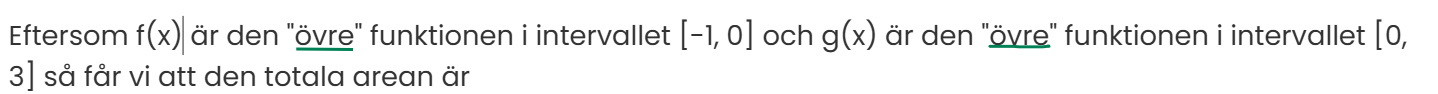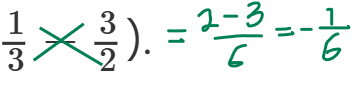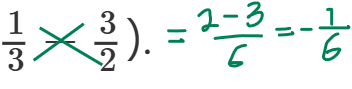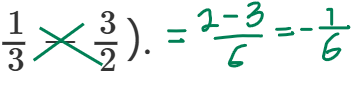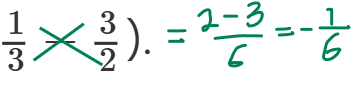Beräkna arean av det sammanlagda området (Matematik/Matte 4/Integraler och tillämpningar)

Förstår inte var nånstans jag gjorde fel

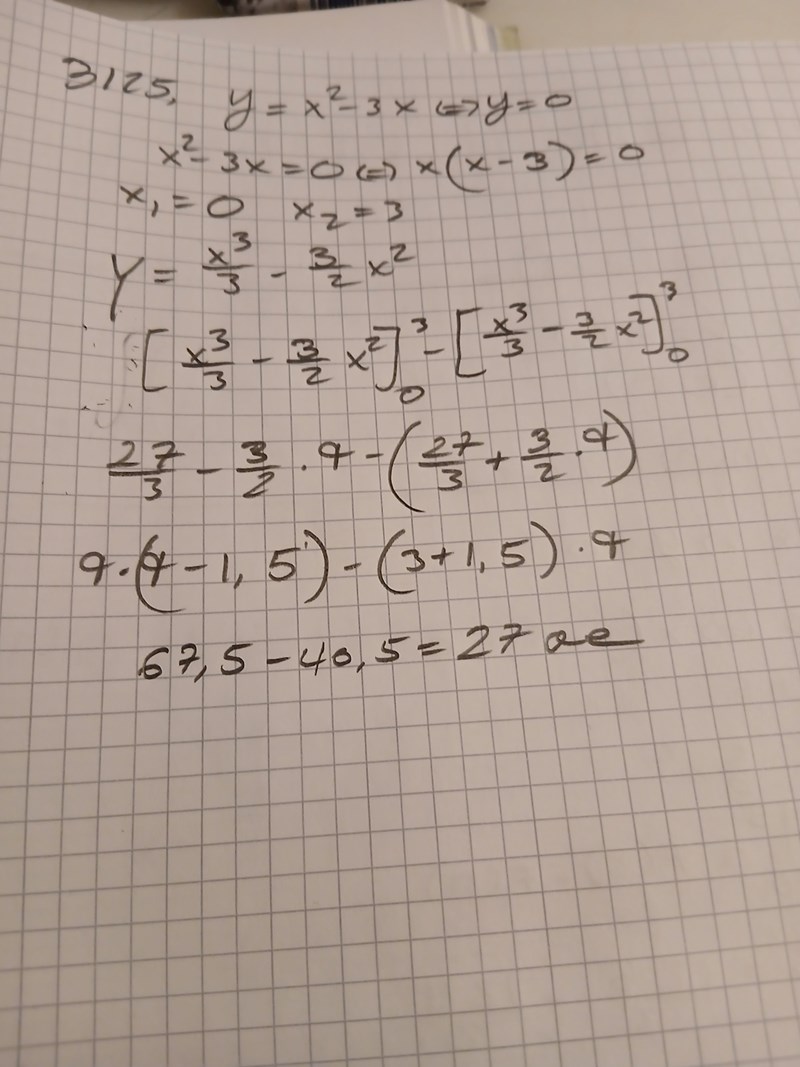
Eller borde jag uttnytja x koordinaten som var givet i uppgiften ?

Tänkte öite annorlunda

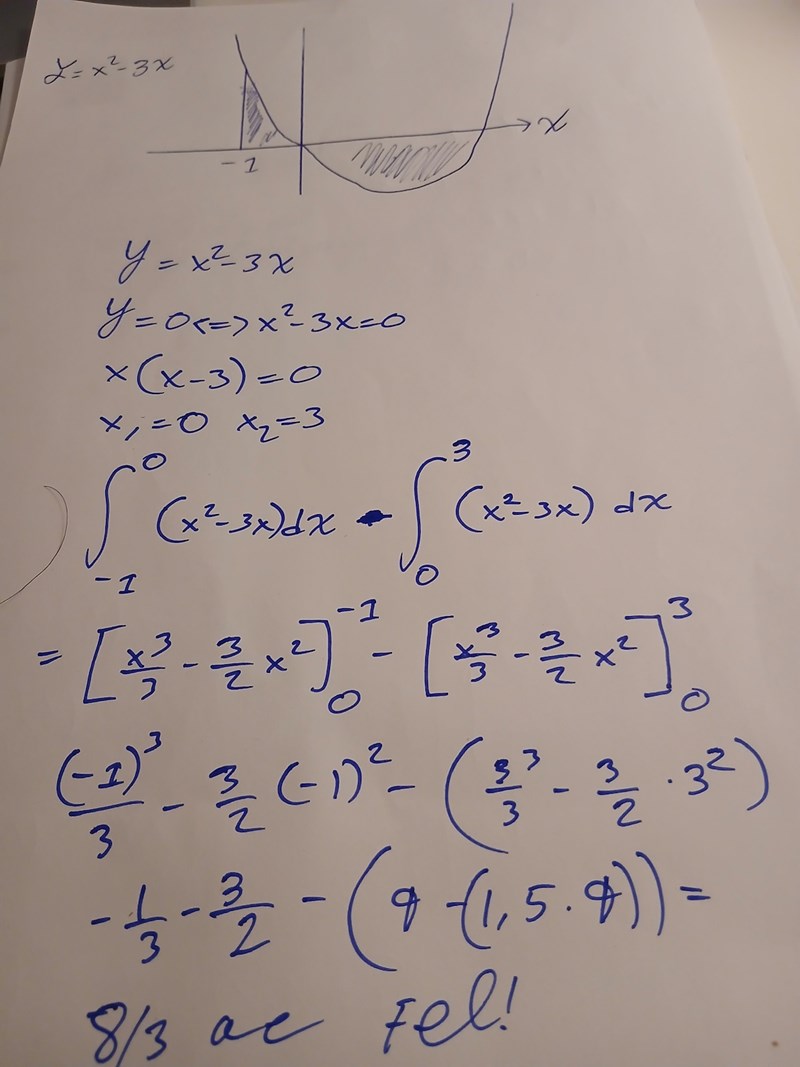
Se ringarna! Egentligen behöver integrationsgränserna inte delas upp.

Ett bra tips för att få till rätt integrand och integrationsgränser i liknande fall är att använda tankesättet man använder för att beräkna arean mellan två grafer.

Då gäller att arean är lika med (integralen av den "övre" funktionen) minus (integralen av den "undre" funktionen), där den "övre" funktionen ligger ovanför den "undre" funktionen.

I detta fallet kan vi tänka att den ena funktionen är g(x) = 0 (vars graf är y = 0, dvs x-axeln).

Vi har alltså att f(x) = x²-3x och g(x) = 0.

Eftersom f(x) är den "övre" funktionen i intervallet [-1, 0] och g(x) är den "övre" funktionen i intervallet [0, 3] så får vi att den totala arean är

$A=A_1+A_2=$

$=\int_{-1}^{0} (f(x)-g(x))\operatorname dx+\int_{0}^{3} (g(x)-f(x))\operatorname dx=$

$=\int_{-1}^{0} ((x^2-3x)-0)\operatorname dx+\int_{0}^{3} (0-(x^2-3x))\operatorname dx=$

$=\int_{-1}^{0} (x^2-3x)\operatorname dx+\int_{0}^{3} -(x^2-3x)\operatorname dx≈$

$=\int_{-1}^{0} (x^2-3x)\operatorname dx-\int_{0}^{3} (x^2-3x)\operatorname dx$

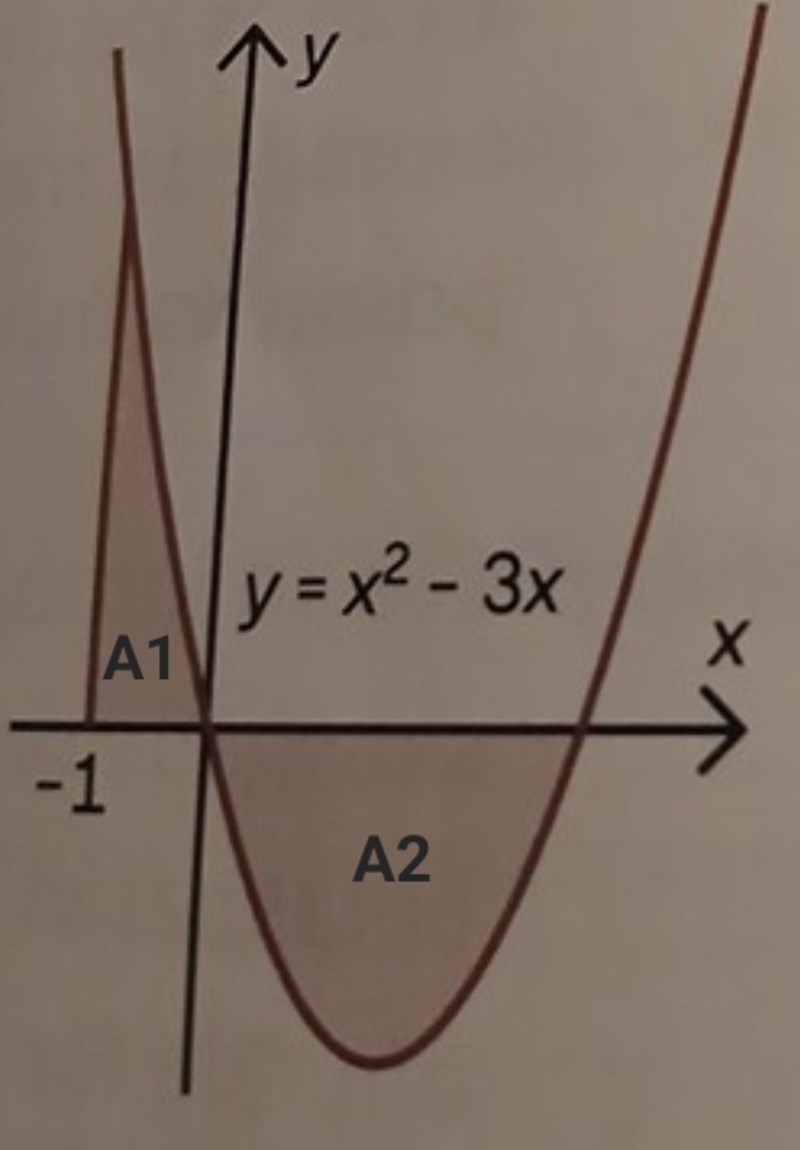
vilken är den övre och undre funktionen. Jag tro du har använt "övre" en gång för mycket det är lite svårt att lista ut vilken som är vilken

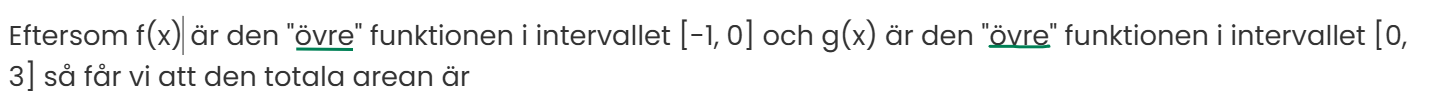
Tillägg: 4 jan 2026 10:59

Jag tolkar det som att $A_{1}$ är min övre funktion eftersom den är ovanför x-axeln och vice.versa när det kommer till $A_{2}$ .

Utöver jag har jag svårt att förstå hur räknereglerna för integraler fungerar

hansa skrev:
Se ringarna! Egentligen behöver integrationsgränserna inte delas upp.

Hur blir det då om man inte delar upp integrationsgränserna ?

Jag gjorde så här, men fick fel svar

Arup skrev:
vilken är den övre och undre funktionen. Jag tro du har använt "övre" en gång för mycket det är lite svårt att lista ut vilken som är vilken

Tillägg: 4 jan 2026 10:59

Jag tolkar det som att $A_{1}$ är min övre funktion eftersom den är ovanför x-axeln och vice.versa när det kommer till $A_{2}$ .

Det som Yngve skrev är korrekt. $f(x)$ är först den övre funktionen. Vid 0 blir $g(x)$ den övre funktionen.

$A_1$ och $A_2$ är inga funktioner utan areor (tal).

---

I din uträkning är det korrekt tills du stoppar in värden. Exempelvis blir din $F(-1)=-1/3-3/2=-11/6$ .

Men innanjag stoppar in behöver jag väl ta den primitiva funktionen

Arup skrev:
Men innanjag stoppar in behöver jag väl ta den primitiva funktionen

Ja, själva beräkningen av integralerna är som vanligt, dvs $\int_{a}^{b}f(x)\operatorname dx=F(b)-F(a)$ , där $F(x)$ är en primitiv funktion till $f(x)$ .

Arup skrev:
vilken är den övre och undre funktionen. Jag tro du har använt "övre" en gång för mycket det är lite svårt att lista ut vilken som är vilken

[...]

Behöver du fortfarande hjälp att identifiera vilken som är den "övre" funktionen och vilken som är den "undre" funktionen?

jag undrar hur hade rätt uppstllning varit?

Jag känner att jag rätt tills jag stoppade in mina värden. Men jag undrar vad var det som gjorde så att jag fick fel svar ?

Arup skrev:
jag undrar hur hade rätt uppstllning varit?

Det går att göra på olika sätt. Jag visade ett sätt i svar #6.

Ett annat sätt är att direkt sätta upp att $A=A_1+A_2$ , där $A_1=\int_{-1}^{0}(x^2-3x)\operatorname dx$ och att $A_2=-\int_{0}^{3}(x^2-3x)\operatorname dx$ .

Minustecknet vid uträkningen av $A_2$ kommer sig av att $A_2$ ligger under x-axeln.

Jag känner att jag rätt tills jag stoppade in mina värden. Men jag undrar vad var det som gjorde så att jag fick fel svar ?

Vilken av dina uträkningar undrar du över?

i #10

Arup skrev:
i #10

Här blev det fel.

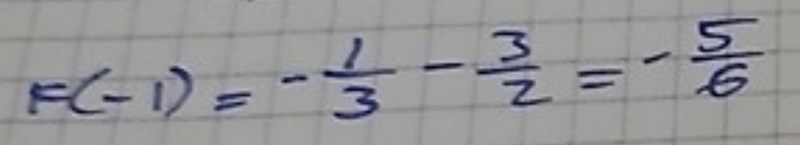
Jag försökte berätta det redan i #11.

jag undrar varför blev det fel. Jag förstod inte riktigt.

Till att börja tog jag den primitiva funktionen dvs $F (x)$ innan jag stoppade in $F (- 1)$

Arup skrev:
jag undrar varför blev det fel. Jag förstod inte riktigt.

Till att börja tog jag den primitiva funktionen dvs $F (x)$ innan jag stoppade in $F (- 1)$

Ditt uttryck för F(x) är rätt, men jag tror att du sedan räknar för mycket i huvudet alternativt att du tar för stora räknesteg i taget.

Beräkna F(-1) igen och skriv ner alla små små steg.

Arup skrev:
jag undrar varför blev det fel. Jag förstod inte riktigt.

Till att börja tog jag den primitiva funktionen dvs $F (x)$ innan jag stoppade in $F (- 1)$

Felet är alltså bara ett räknefel med bråken. Inget konceptuellt med integralerna. De har du löst!

ok vi har:

$f (x) = x^{2} - 3 x F (x) = \frac{x^{3}}{3} - \frac{3}{2} x^{2} F (- 1) = \frac{{(- 1)}^{3}}{3} - \frac{3}{2} {(- 1)}^{2} F (- 1) = \frac{1}{3} - \frac{3}{2} \leftrightarrow F (- 1) = - \frac{1}{6}$

Nej, det blir

$\displaystyle -\frac{1}{3} -\frac{3}{2} = -\frac{2}{6} -\frac{9}{6}=-\frac{11}{6}$ .

$(-1)^3=-1$

aha just det slarvfel

Jag blir lite oroad av att det återigen blev fel när du skulle subtrahera två bråk från varandra (först vid beräkningen av $-\frac{1}{3}-\frac{3}{2}$ och sedan vid beräkningen av $\frac{1}{3}-\frac{3}{2}$ ).

Jag tror att det beror på att du tar för stora räknesteg I taget och/eller att du räknar i huvudet istället för på papper.

Kan du visa, steg för steg, hur du beräknar t.ex. $\frac{1}{3}-\frac{3}{2}$ . Ta med alla steg som jag bad dig göra tidigare, dvs gemensam nämnare, gemensamt bråkstreck, förenkla täljare o.s.v?

Asså jag tror anledning till att får fel är för att jag korsvisar multiplicerar bråken i huvudet såhär:

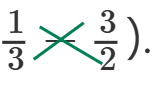
Det här var ett trick jag lärde mig från en anhörig länge sen för att det skulle spara tid och det skulle göra mig bättre på huvud räkning.

Men då får du ju inte glömma din multiplikation av 3orna! :)

Arup skrev:

de här är fel det ska bli :

$\frac{1}{3} - \frac{3}{2} m g n = 6 (\frac{1}{3} \times \frac{2}{2}) - (\frac{3}{2} \times \frac{3}{3}) = \frac{2}{6} - \frac{9}{6} = - \frac{7}{6}$

jag såg misstolade 3:an för en två så det skulle bli $3 \times 3$

Den uträkningen stämmer ja. Men i frågan är det fortfarande -11/6 som gäller.

Arup skrev:
Arup skrev:

de här är fel det ska bli :

$\frac{1}{3} - \frac{3}{2} m g n = 6 (\frac{1}{3} \times \frac{2}{2}) - (\frac{3}{2} \times \frac{3}{3}) = \frac{2}{6} - \frac{9}{6} = - \frac{7}{6}$

Bra, nu är det rätt.

Kom ihåg att alltid göra så.

Tricket du lärde dig av en anhörig funkar bara för specialfallet att båda täljarna är lika med 1.

Eller att tricket egentligen var "korsvis multiplikation" med nämnarna, vilket fungerar. Men då måste du komma ihåg att multiplicera respektive täljare med nämnarna, vilket är lätt att missa om man tar för stora räknesteg och/eller räknar i huvudet istället för på papper

Yngve skrev:
Arup skrev:
Arup skrev:

de här är fel det ska bli :

$\frac{1}{3} - \frac{3}{2} m g n = 6 (\frac{1}{3} \times \frac{2}{2}) - (\frac{3}{2} \times \frac{3}{3}) = \frac{2}{6} - \frac{9}{6} = - \frac{7}{6}$

Bra, nu är det rätt.

Kom ihåg att alltid göra så.

Tricket du lärde dig av en anhörig funkar bara för specialfallet att båda täljarna är lika med 1.

Eller att tricket egentligen var "korsvis multiplikation" med nämnarna, vilket fungerar. Men då måste du komma ihåg att multiplicera respektive täljare med nämnarna, vilket är lätt att missa om man tar för stora räknesteg och/eller räknar i huvudet istället för på papper

Ja, du har rött jag korsvis multiplicerar bråken i huvdet och undviker mgn

Arup skrev:

Ja, du har rött jag korsvis multiplicerar bråken i huvdet och undviker mgn

OK, att korsvis multiplicera täljare med nämnare fungerar bra, men jag vill då råda dig att tills vidare undvika huvudräkning. Det tar marginellt längre tid att skriva en uträkning vid sidan av, men det minskar risken för räknefel rejält.

=====

Kommentar: Korsvis multiplikation ger alltid en gemensam nämnare, men inte alltid den minsta gemensamma nämnaren.

Exempel:

1/2+2/3 = (1*3)/(2*3)+(2*2)/(3*2) = 3/6+4/6 ger gemensam nämnare 6, vilket även råkar vara den minsta gemensamma nämnaren.
3/4+1/6 = (3*6)/(4*6)+(1*4)/(6*4) = 18/24+4/24 ger gemensam nämnare 24, men detta är inte den minsta gemensamma nämnaren.

Förstår, men jag kan jun alltid förkorta/förlänga bråket för att få det i enklast form

Arup skrev:
Förstår, men jag kan jun alltid förkorta/förlänga bråket för att få det i enklast form

Japp, det går bra.

Korsvis multiplikation är alltså en utmärkt metod för att beräkna summor/differenser av bråktal, så länge som det rör sig om hyfsat små tal.

=====

Exempel:

Om vi har 210/1470+36/180 så bör man nog istället börja med att förkorta bråktalen varflör sig innan man ger sig på gemensam nämnare.

ok, om vi tänker oss att vi har $\frac{2}{25}$

skulle jag nog ha förlängt med 4

$\frac{2}{25} \times \frac{4}{4} = \frac{8}{100}$

Arup skrev:
ok, om vi tänker oss att vi har $\frac{2}{25}$

skulle jag nog ha förlängt med 4

$\frac{2}{25} \times \frac{4}{4} = \frac{8}{100}$

Ja, 2/25 är lika med 8/100.

Men vad du ska förlänga med beror på hur du tänker använda talet.

Om du t.ex. ska addera 2/25 med 3/4 så kan det vara en bra idé att förlänga det första bråket med 4 och det andra bråket med 25.

Men om du ska addera 2/25 med 3/5 så behöver du inte förlänga det första bråket alls utan det räcker då att förlänga det andra bråket med 5.

Yngve, är du fortfarande orolig över bråkräkning ?

Jag tror anledningen till att jag fick fel var inte för att jag inte kan.

Arup skrev:
Yngve, är du fortfarande orolig över bråkräkning ?

Jag tror anledningen till att jag fick fel var inte för att jag inte kan.

Nej, jag vet att du kan. Och jag tror att felorsaken var att du tog för stora äknesteg i taget och/eller räknade i huvudet istället för på papper.