Byte av integrationsgränser (Fubini)

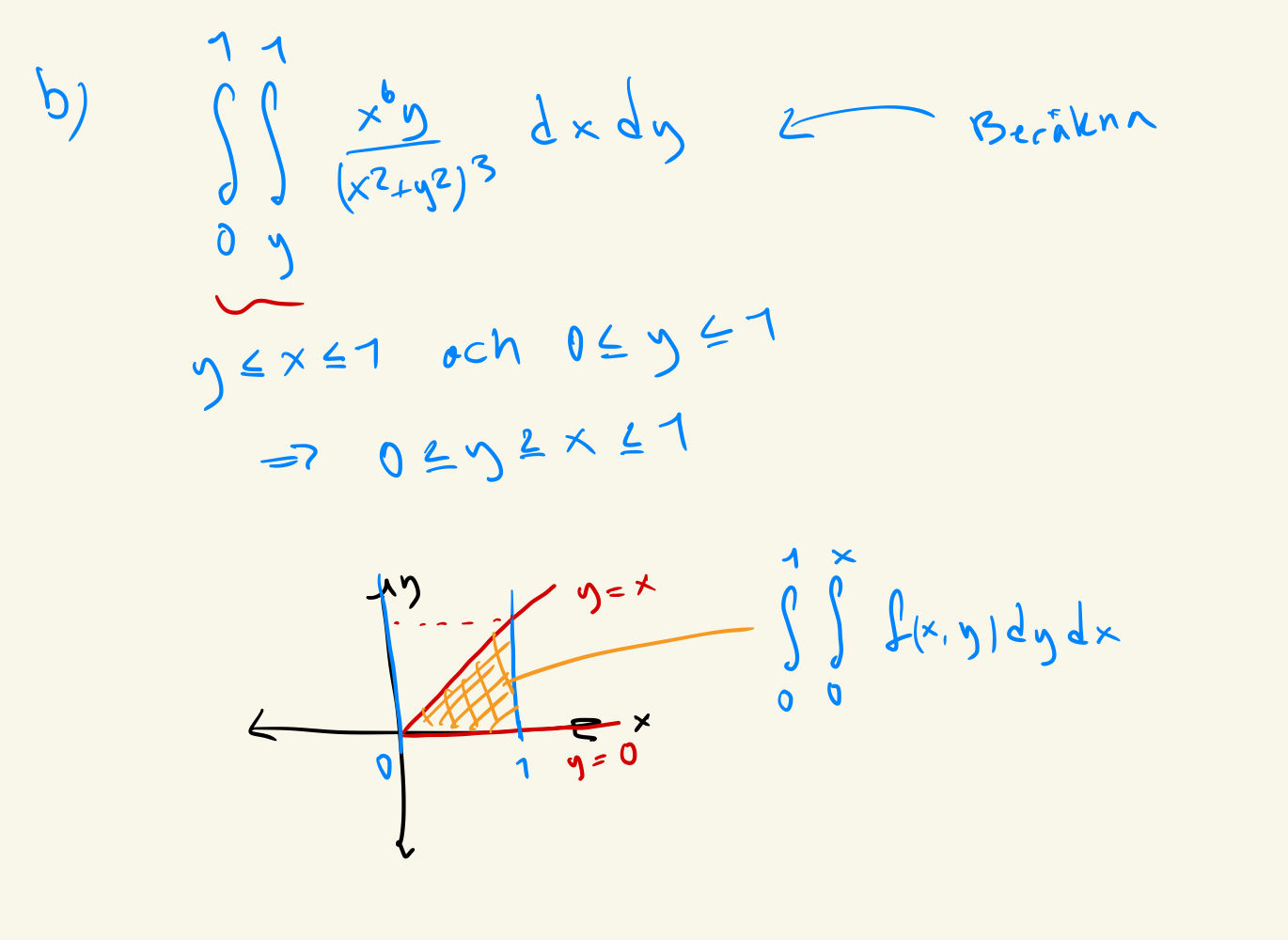
Okej, det är självklart inte korrekt att skriva att hela dubbelintegralen är det området, men att basytan för dubbelintegralen är det området?

Ja, jag tycker att du har uppfattat området korrekt. Och det blir såklart en enkel integral.

Men kan du verkligen med gott samvete motstå frestelsen att övergå till polära koordinater? :)

Döm mig inte. Detta var träning med Fubini! 

En annan metod som vi använder är med nivårkurvor. Den fungerar när integranden är på formen h(f(x,y)). Helt sjuk metod men jag fattar ingenting. Lär bli att jag återkommer angående den. 

Tack för hjälpen! :)

Eller vänta, hur skulle du smidigt lösa gränserna för sfäriska koordinater här?

Mja, smidigt blir det kanske inte, men lite roligt. När det gäller vinkeln visar din skiss av området att $\theta$ ska löpa från $0$ till $\pi/4$, linjen $y=x$ lutar 45°. Men om det är oklart att du ställa upp dina gränser som olikheter.

$0<y<x \iff 0<r\sin(\theta)<r\cos(\theta)$

Delar vi med det positiva talet (första kvadranten) $r\cos(\theta)$ får vi

$0<\tan(\theta)<1$

$0<\theta<\pi/4$

Med samma resonemang inser vi att

$0<x<1 \iff 0<r\cos(\theta)<1$

$0<r<\frac{1}{\cos(\theta)}$

Nu ställer vi upp integralen och förenklar samt integrerar i r-led. Glöm inte bort den extra skalfaktorn $r$:

$\displaystyle \int_{\theta=0}^{\pi/4} \int_{r=0}^{1/\cos(\theta)}r^8 \cos^6\left(\theta\right)\sin\left(\theta\right)/r^6\,drd\theta=\frac13 \int_{\theta=0}^{\pi/4}\cos^3\left(\theta\right)\sin\left(\theta\right)d\theta$

Slutligen låter vi $t=\sin\left(\theta\right),\, dt=\cos\left(\theta\right)d\theta$ och erhåller

$\displaystyle \int_0^{1/\sqrt2} t\left(t^2-1\right)dt=\frac{1}{16}$

Jaha, okej. Lite oklart varför jag inte såg det själv. Tack!