c^2=a^2+b^2, hyperbel

Nu har du väl ändå skrivit fel? Kurvan a²+b²=c² (eller vanligare r²) är en cirkel, inte en hyperbel.

Smaragdalena skrev:

Nu har du väl ändå skrivit fel? Kurvan a²+b²=c² (eller vanligare r²) är en cirkel, inte en hyperbel.

Du har missuppfattat vad $a$, $b$ och $c$ står för. $a$ och $b$ är konstanterna i hyperbelns ekvation $x^2/a^2-y^2/b^2=1$ och $c$ är $x$-koordinaten för fokus. (Dock säger jag inte att cirklar inte har något med saken att göra :-))

Till lamayo: det finns många olika definitioner av en hyperbel. Kan du kanske länka till beviset du kollar på så att vi förstår vad man utgår ifrån?

Hyperbelns form bestäms av dess fokus och vertex.

Med fokus i (±c,0) och vertex i (±a,0) så är det parametrarna a och c (där c > a) som bestämmer formen.

Se t.ex här under Hyperbola in Cartesian coordinates hur parametern b relaterar till a och c.

AlvinB skrev:

Smaragdalena skrev:

Nu har du väl ändå skrivit fel? Kurvan a²+b²=c² (eller vanligare r²) är en cirkel, inte en hyperbel.

Du har missuppfattat vad $a$, $b$ och $c$ står för. $a$ och $b$ är konstanterna i hyperbelns ekvation $x^2/a^2-y^2/b^2=1$ och $c$ är $x$-koordinaten för fokus. (Dock säger jag inte att cirklar inte har något med saken att göra :-))

Till lamayo: det finns många olika definitioner av en hyperbel. Kan du kanske länka till beviset du kollar på så att vi förstår vad man utgår ifrån?

https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/deriving-the-equation-of-a-hyperbola-centered-at-the-origin/

Dr. G skrev:

Hyperbelns form bestäms av dess fokus och vertex.

Med fokus i (±c,0) och vertex i (±a,0) så är det parametrarna a och c (där c > a) som bestämmer formen.

Se t.ex här under Hyperbola in Cartesian coordinates hur parametern b relaterar till a och c.

Hur kan man bara sätta b^2=c^2-a^2? hittar inte någon förklaring där?

Grejen är väl den att hyperbeln beskrivs fullständigt av två konstanter (relativt "sitt" koordinatsystem). Dessa kan t.ex vara a och c, eller a och b.

För en ellips har b en tydlig geometrisk tolkning, (halva lillaxelns längd) medan så inte är fallet för en hyperbel. (Om någon anser att detta är felaktigt så säg gärna till.)

Givet a och c så är b helt enkelt

$b=\sqrt{c^2-a^2}$

Dr. G skrev:

Grejen är väl den att hyperbeln beskrivs fullständigt av två konstanter (relativt "sitt" koordinatsystem). Dessa kan t.ex vara a och c, eller a och b.

För en ellips har b en tydlig geometrisk tolkning, (halva lillaxelns längd) medan så inte är fallet för en hyperbel. (Om någon anser att detta är felaktigt så säg gärna till.)

Givet a och c så är b helt enkelt

$b=\sqrt{c^2-a^2}$

men om det inte finns någon geometrisk tolkning, hur kom man fram till det?

Från härledningen på t.ex Wikipedia kan du skriva hyperbelns ekvation som

$\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}= 1$

Inför en ny konstant b^2 = c^2 - a^2,

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}= 1$

Dr. G skrev:

Från härledningen på t.ex Wikipedia kan du skriva hyperbelns ekvation som

$\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}= 1$

Inför en ny konstant b^2 = c^2 - a^2,

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}= 1$

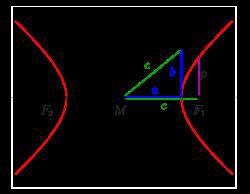
aha okej, trodde a,b och c fanns i hyperbeln, men uppfattade bilden nedan fel. Tack!!

De linjära asymptoterna har lutning

$k= \frac{b}{a}=\frac{\sqrt{c^2-a^2}}{a}$

så det är väl en geometrisk innebörd av b, dock inte lika direkt som i ellipsfallet, tycker jag.

Dr. G skrev:

De linjära asymptoterna har lutning

$k= \frac{b}{a}=\frac{\sqrt{c^2-a^2}}{a}$

så det är väl en geometrisk innebörd av b, dock inte lika direkt som i ellipsfallet, tycker jag.

jaha det är därifrån det kommer, tack så mycket!! :)

Kan man också härleda sambandet geometriskt utifrån ovanstående bild? Där ser man ju att c^2=a^2+b^2. Fungerar det som ett alternativt bevis till att använda asymptoter?

Dr. G skrev:

De linjära asymptoterna har lutning

$k= \frac{b}{a}=\frac{\sqrt{c^2-a^2}}{a}$

så det är väl en geometrisk innebörd av b, dock inte lika direkt som i ellipsfallet, tycker jag.

Måste bara fråga, varför är k=sqrt(c^2-a^2)/a? Förstår att k=b/a.

Dr. G skrev:

Från härledningen på t.ex Wikipedia kan du skriva hyperbelns ekvation som

$\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}= 1$

Inför en ny konstant b^2 = c^2 - a^2,

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}= 1$

Från härledningen så ser man att 

$b^2 = c^2 - a^2$.

Det finns ju två asymptoter, så det ska vara

$k = \pm \dfrac{b}{a}$

ifall det inte framgick.

Dr. G skrev:

Dr. G skrev:

Från härledningen på t.ex Wikipedia kan du skriva hyperbelns ekvation som

$\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}= 1$

Inför en ny konstant b^2 = c^2 - a^2,

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}= 1$

Från härledningen så ser man att 

$b^2 = c^2 - a^2$.

Det finns ju två asymptoter, så det ska vara

$k = \pm \dfrac{b}{a}$

ifall det inte framgick.

Hur ser man att b^2=c^2-a^2 från härledningen?

Så här:

Man tycker att $c^2-a^2$ är krångligt att skriva. Därför har man bestämt att införa en ny konstant $b$ sådan att $b^2=c^2-a^2$ för att göra det lättare att arbeta med.

AlvinB skrev:

Så här:

Man tycker att $c^2-a^2$ är krångligt att skriva. Därför har man bestämt att införa en ny konstant $b$ sådan att $b^2=c^2-a^2$ för att göra det lättare att arbeta med.

Aha, så det är inget man härleder. Tack för hjälpen!