Cirkel- och kaströrelse

Hej igenn! Jag behöver hjälp med även denna uppgift.

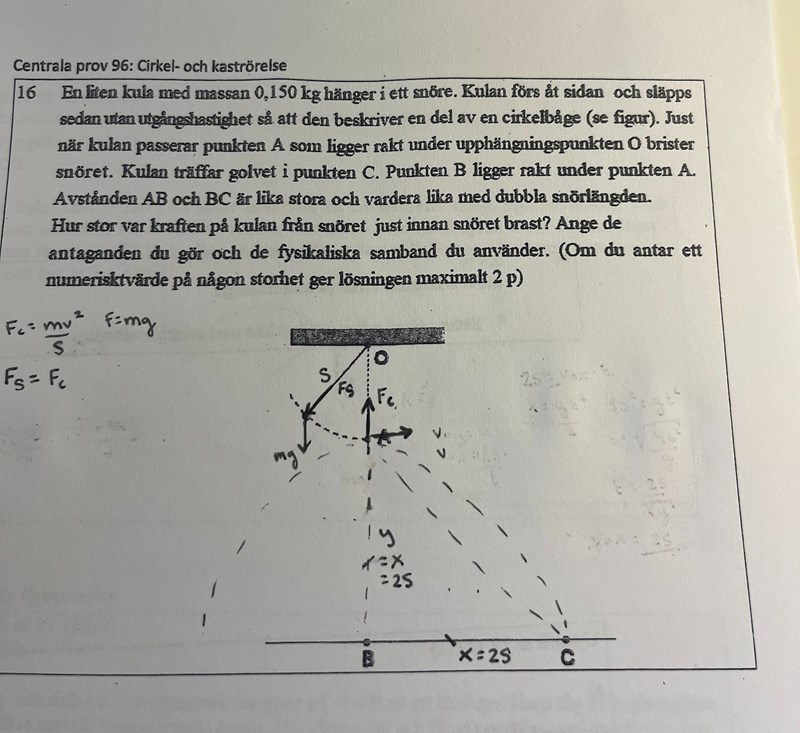
Jag tänker såhär: på snöret när det bryter verkar Fc uppåt mot cirkelns centrum, tyngdkraften nedåt och en spännkraft på kulan från snöret nedåt,

dvs. Fc = Fs + mg

(mv²)/r= Fs + mg, där r=snörets längd.

Vi vill veta Fs då snöret bryts, alltså; Fs = (mv²/r) - mg

För att få reda på v behöver vi använda formler för kaströrelse.

x=vo_x t, och y=Vo_yt + (at²)/2

Vi vet att avståndet AB, dvs fallhöjden y, och avståndet BC, dvs. kaststräckan x, är lika långa och dubbla snörets längd. Det ger oss: x=y=2r.

Härifrån kommer jag inte längre... hur ska jag komma vidare?

$F_s$ drar i kulan uppåt så den kraften är riktad uppåt.

Du är på god väg. Det kan vara bra att sortera upp vad man vet och vad man söker. Det enda vi saknar för att beräkna $F_s$ är hastigheten i A, alltså $v_{0x}$ . Jag skulle nog använda att $2r=v_{0x}t$ ger oss att $t=\frac{2r}{v_{0x}}$ som vi kan sätta in i din andra formel där $v_{0y}=0$ och $a=-g$ .

Okej! Så jag kan fortsätta såhär:

2r=Vo_xt

t=(2r)/Vo_x (1)

y= 0 - (gt²)/2 (2)

insätter (1) i (2): y= - g(4r²/Vo_x²)/2

y=2r= - (g4r²)/(2Vo_x)

2Vo_x x 2r = -g x 4r² (x'en är gånger :))

Vo_x= - (g2r²) / (4r)

Vo_x = -gr

Hur blir kraftsambandet när Fs verkar upp? Blir Fc + Fs = mg? I ett föregående inlägg hjälpte du mig med en cirkelrörelse, och påstod då att Fc benämns som den resulterande kraften innåt. Är det rätt att säga att Fc är lika med Fr, och därmed Fs-mg? Dvs. Fc=Fs-mg. Då blir energisambandet istället Fs=Fc+mg.

Fs= (mv²)/r + mg

Fs= (mVo_x²)/r + mg

Fs= (m(-gr)²)/r + mg

Fs= (mg²r) + mg

Massan vet vi ur uppgiften, m=0,15kg, och a=gravitationskraften 9,82m/s². Då saknar vi r, snörets längd. Stämmer detta vidare resonemang?

Jag svarar på frågorna med en bild:

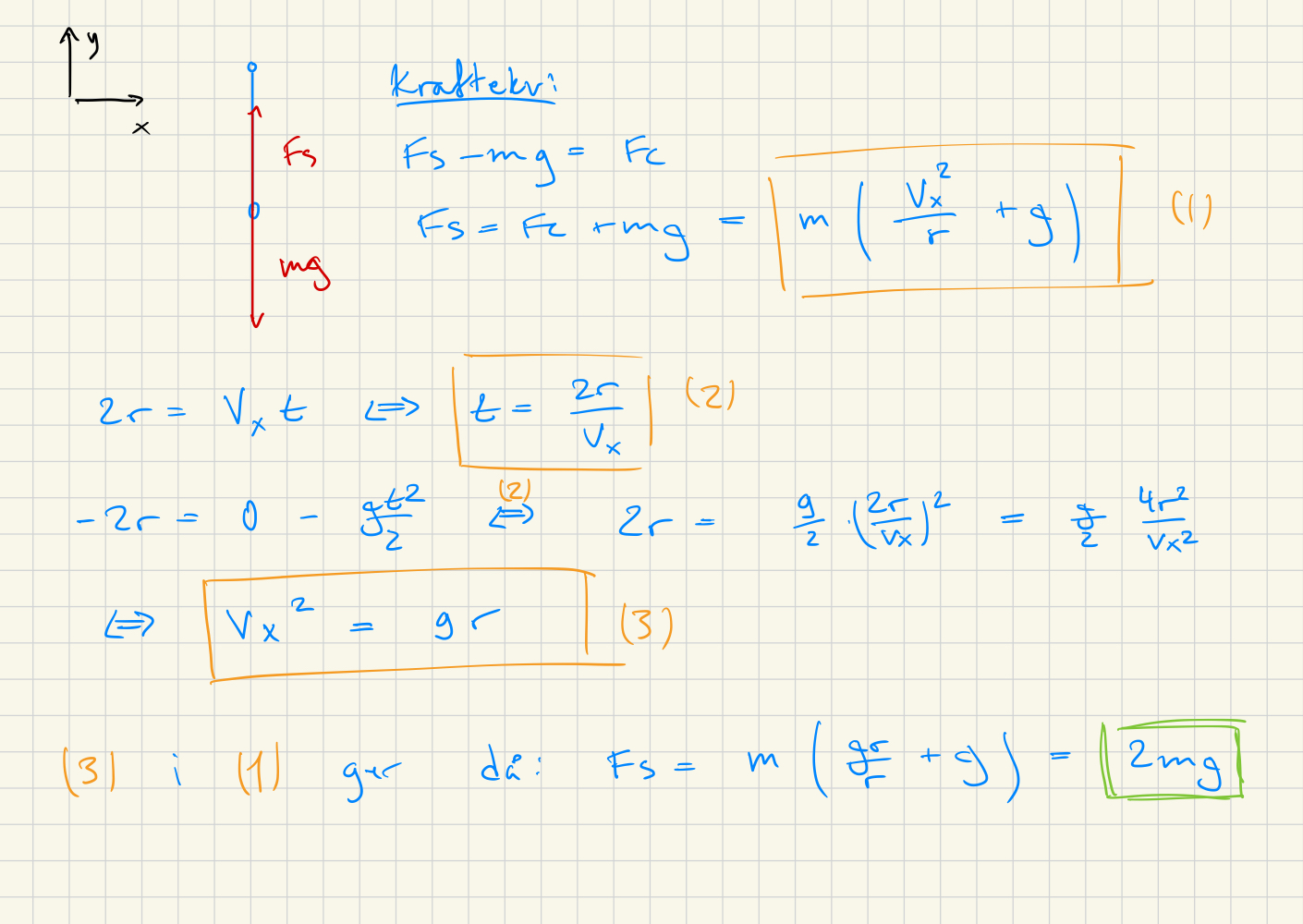
Tack så hemskt mycket MrPotatohead, nu förstår jag! Du är guld värd!!

Om man tänker med centrifugalkraft kan man också tänka sig att krafterna borde adderas i bottenlägget. Tänk dig att du gungar. I bottenlägget så känner man att snörena spänner sig mer än när man är uppe på sidorna. Det beror just på att hela $mg$ verkar längs snöret plus den fiktiva centrifugalkraften i den punkten.

Vad bra att du förstår! :) Personligen missuppfattade jag hur centripetalkraft fungerade alldeles för länge..

Svara

Visa senaste svar