Cirkulär centralrörelse
Hej! Jag vet inte riktigt hue jag ska lösa f) uppgiften. Jag vet att jag bör ställa ekvationer för x- och y-led och använda mig av kaströrelse, däremot vet jag inte hur jag ska börja. Hur ska kraftfiguren ut? Tack på förhand!
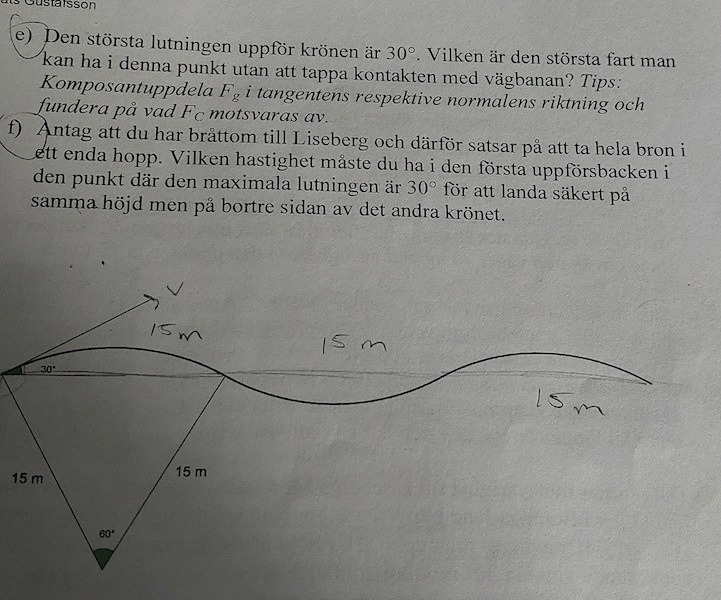

För den horisontella sträckan så har vi
sx = v•cos(30˚)•t
Vid tiden t = T är sx = 3•15 = 45 m
Då har vi 45 = v•(√3/2)•T
Vertikala hastigheten vy = v•sin(30˚) - g•t
Vid tiden T gäller då att (-v)•(1/2) = v•(1/2) - g•T
som ger att
v = g•T = g•2•45/(√3•v)
v2 = 90•g/√3 = 3•g√300 ≈ 30•17,3 = 519
v = √519 = √(529-10) ≈ 23 m/s = 23•3,6 ≈ 83 km/h
Tack! Jag hängde med såhär långt, därefter slutade jag förstå hur du gjorde din beräkning. 😅 
För en kastparabel som startar från marknivå och som slår ner i marknivå, så är den horisontella hastigheten hela tiden densamma, medan den vertikala nedslagshastigheten har samma belopp, men med ombytt tecken.
Jag hänger inte riktigt med.. Vi ställde först upp ett uttryck för x-led där horisontella sträckan motsvarar 45 = v0 * cos(30)* t. Sedan ställde vi upp ett uttryck för hastigheten i y-led: v0 * sin (30) = V0y* sin (30).
Enligt det du säger bör alltså hela -(v0 * sin (30) = V0y* sin (30)) även vara hastigheten i x-led utan minustecknet?
Ritar man det som ett v-t diagram blir det ungefär som följande:




