Cirkulär pool (volym)
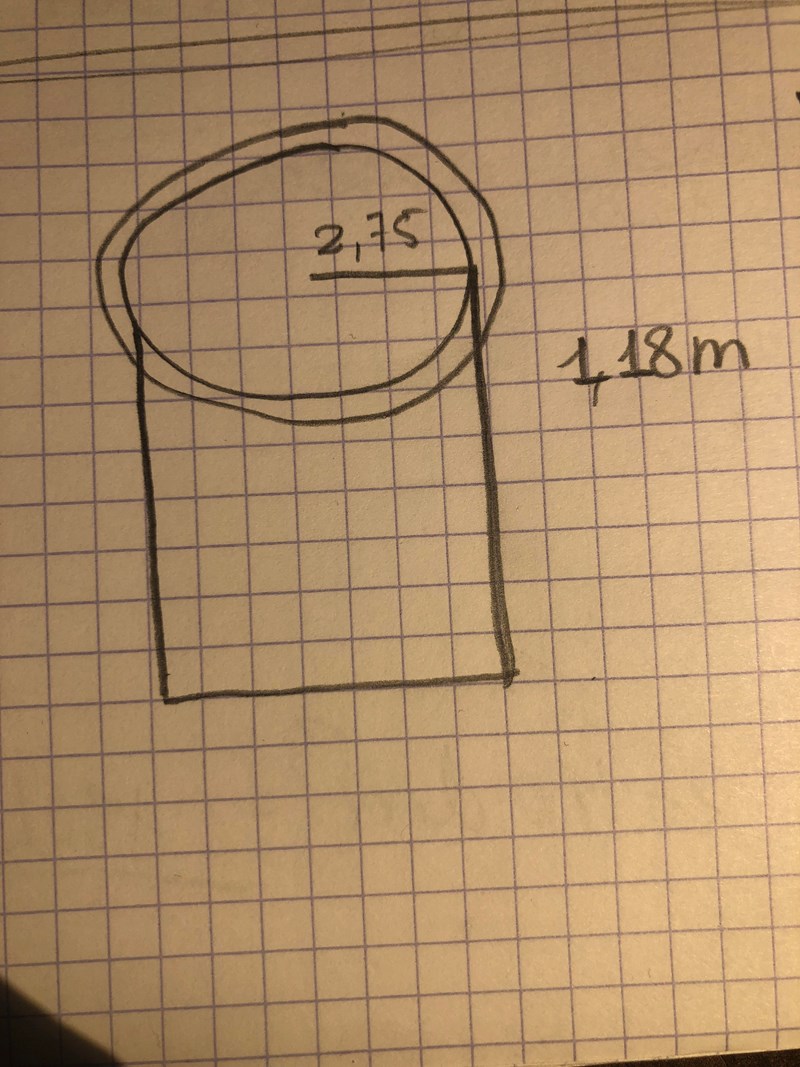
Cirkulär pool med radie 2,75m och vattendjup 1,18m. Avståndet mellan vattenytan och poolkanten är 0,06m. Varje år fylls poolen från två vattenslangar som vardera ger 20 liter per minut. pris för vattnet är 16kr/m^3
A) Hur lång tid tar det att fylla poolen? svara i hela timmar
B) Hur många människor måste samtidigt vara i vattnet (helt neddoppade) för att vattnet ska rinna över poolkanten. räkna med att en människa har en volym på 70 liter.
Min lösning :
B) Jag tänkte att det ska vara 2 cylindrar, den lilla i den stora som en ring. StorCylindervolym-LillaCylindervolym=volymen av bassängen
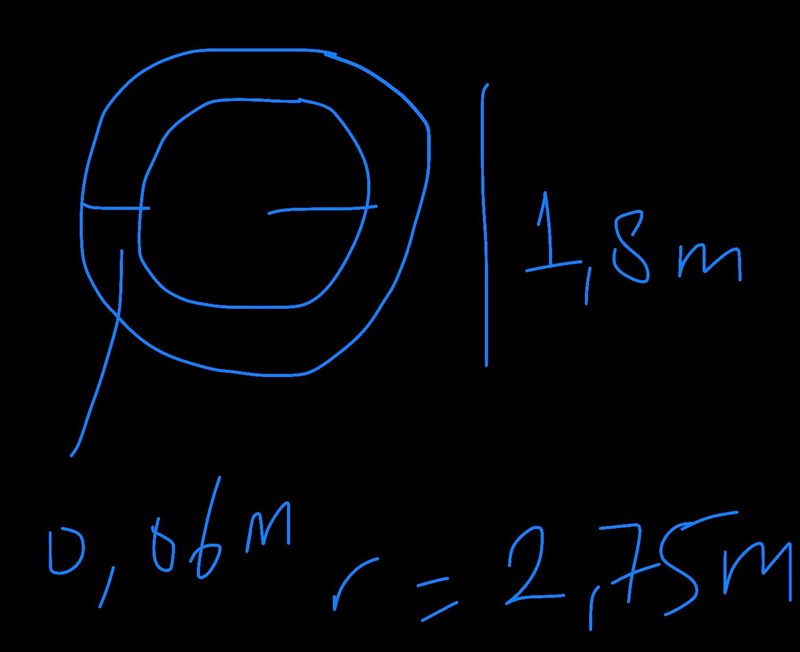 ungefär så tänker jag. Dock så fick jag fel svar.
ungefär så tänker jag. Dock så fick jag fel svar.
CylinderSTOR: (2,75*2)+(0,06*2)/2=3,35m=radie
volym : 3,35^2*pi*1,18=RÅKADE RITA FEL MEN JAG RÄKNAR MED HÖJDEN 1,18M)=41,6m^3
CylinderLITEN: 2,75^2*pi*1,18=28m^3
volymen för bassängen blir 41,6-28=13,6m^3=14m^3
70L=0,07m^3
x=antal personer
0,07x=14
x=200
om det blir mer än 200 pers så kommer vattnet att rinna. I facit står det 20pers vilket jag inte ens fattar.
Varför ritar du två ringer? Det står inte i uppgiften. Dret står bara att poolen är formad som en cylinder med radien 2,75 meter och djupet 1,18 m. (Det du har ritat heter en cylinder-ring).
Avståndet mellan vattenytan och poolkanten räknas rakt upp. Hur bred poolen är i sin konstruktion spelar ingen roll, vi har fått veta innerdiametern.
Smaragdalena skrev:Varför ritar du två ringer? Det står inte i uppgiften. Dret står bara att poolen är formad som en cylinder med radien 2,75 meter och djupet 1,18 m. (Det du har ritat heter en cylinder-ring).
För att det också står ”Avståndet mellan vattenytan och poolkanten är 0,06m” . Jag räknar ut att volymen är 28m^3
B) 70L=70dm^3=0,07m^3
X max antal personer
0,07x=28
x=400personer
A) 0,04x=28
x=700min=12h . Det tar 12h
Vad ska jag göra med 0,06m? Jag har svårt att förstå varför0,06 är med djupet. I en tidigare uppgift (ganska lik) var det en tjocklek som man hade kallat 0,06m för. Varför kan man inte kalla den för en tjocklek?
Nu när du ser att din första ritning var fel, gör en ny så tittar vi på den. (Det var mycket bra att du gjorde en ritning direkt.)
Du behöver de där sex centimeterna till b-uppgiften. När tillräckligt många personer kliver ner i poolen,kommer vattnet att rinna över (eftersom människorna tar plats och tränger undan vattnet). Det rinner över när vattenytan har höjts 6 cm.
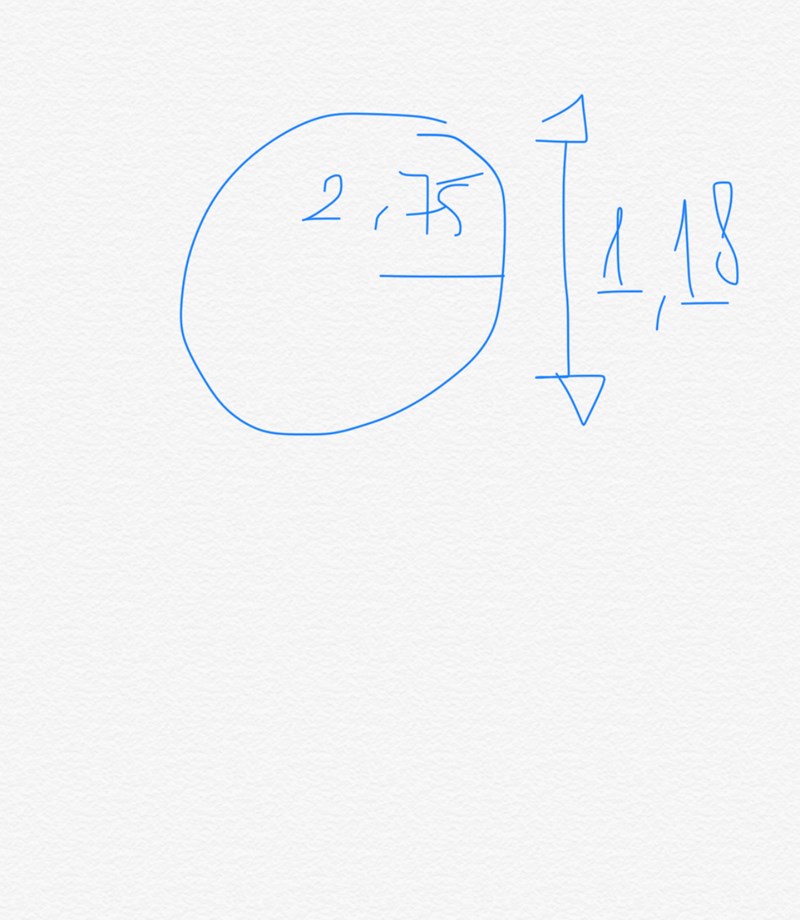 Jag förstår inte. Det står att det är 0,06m mellan vattenytan och poolkanten. Vad ska den här 0,06m föreställa och vart ska jag rita den i min nya bild? Hur kan bilden annars se ut så att det blir enklare att förstår uppgiften?
Jag förstår inte. Det står att det är 0,06m mellan vattenytan och poolkanten. Vad ska den här 0,06m föreställa och vart ska jag rita den i min nya bild? Hur kan bilden annars se ut så att det blir enklare att förstår uppgiften?
De 6 centimeterna är ovanför (den cirkulära) vattenytan.
Kan du visa med en bild,snälla? Förstår inte :(((
För att visa vad som är ovanför måste du rita poolen från sidan.
Förstår inte hur jag ska rita poolen från sidan?? :(( menar du att jag ska rita halva polen.?
Poolen är en cylinder. Du måste ha sett cylindrar ritade från sidan.
Så här brukar man rita en cylinder från sidan.
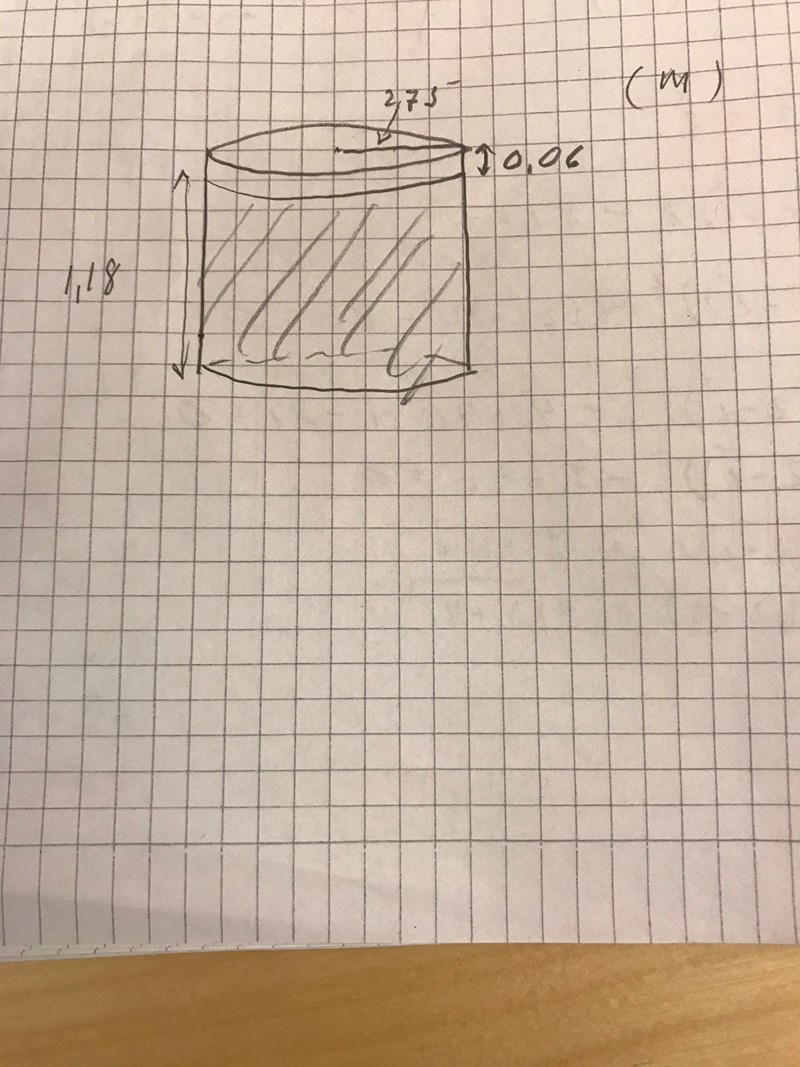
Ok man ska alltså beräkna volymen av hela cylindern
Nu har någon varit snäll och ritat en bild där 0,06 står med, så slapp du göra det. Nu kan vi fortsätta där vi var för ett tag sen. Förstår du måttet 0,06 nu?
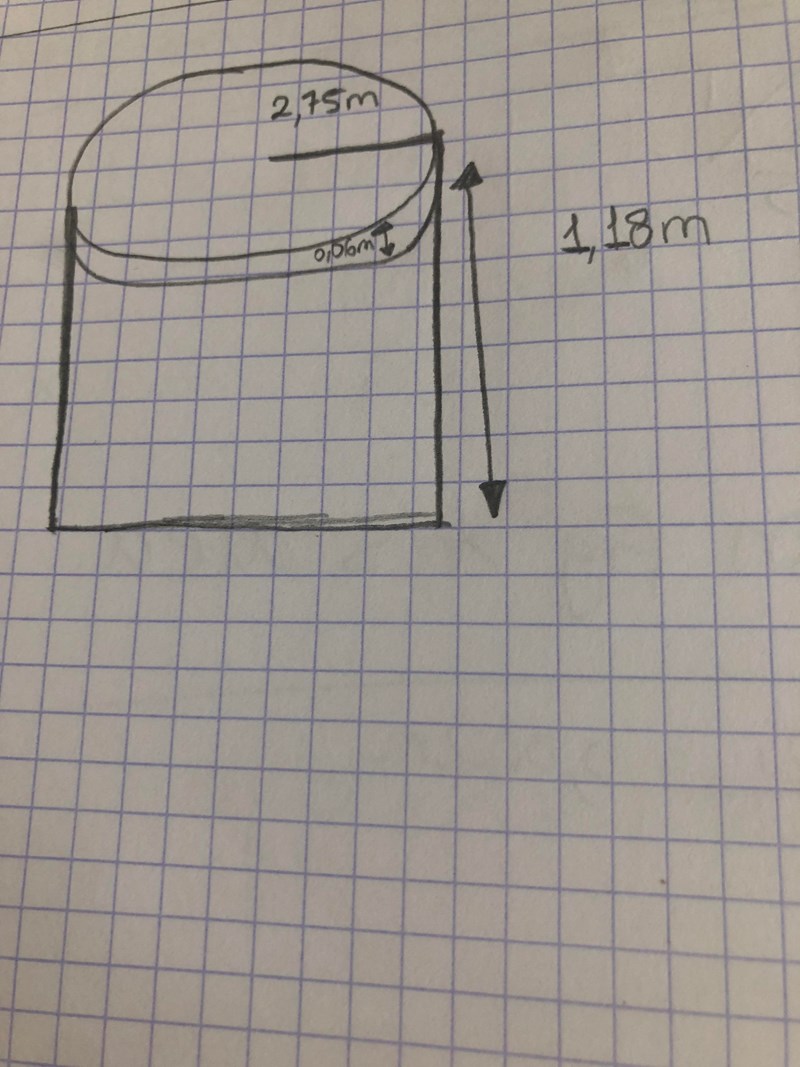
såhär ser poolen, metallbitarna ovanför motsvarar ”0,06m” om jag har förstått rätt? Jag tänkte tvärtom  jag tänkte att kanten ”som är 0,06m” skulle se ut så här 2 cylindrar.
jag tänkte att kanten ”som är 0,06m” skulle se ut så här 2 cylindrar. 
Kanten som är 6 cm är avståndet från vattenytan och upp till poolens överkant. På din övre pool kommer det att rinna över en stund innan det skulle nå upp till de övre rören, eftersom det är ett hål under varje "korsning".
Det är tydligt att det du behöver träna mest på för att bli bättre på matte är läsförståelse.
peono skrev:Så här brukar man rita en cylinder från sidan.
Ok, volymen för bassängen/poolen blir : 1,24*2,75^2*pi=29m^3
70L=0,07m^3
0,07x=29
x antal personer poolen rymmer max
x=414
vart är felet?
Smaragdalena skrev:Kanten som är 6 cm är avståndet från vattenytan och upp till poolens överkant. På din övre pool kommer det att rinna över en stund innan det skulle nå upp till de övre rören, eftersom det är ett hål under varje "korsning".
Det är tydligt att det du behöver träna mest på för att bli bättre på matte är läsförståelse.
Jag håller faktiskt med. Men jag vet tyvärr inte hur jag ska förbättra läsförståelsen. Har försökt läsa böcker men det hjälper inte
B-frågan handlar om hur mänga människor som behöver kliva ner i vattnet för att vattenytan skall höjas 6 cm, så att vattnet börjar rinna över kanten. Hur stor volym har "vattenskivan" som har samma area som poolen och är 6 cm tjock? Hur många 70liters-personer behövs det för att de sammanlagt skall ha lika stor volym som "vattenskivan"?
För läsförståelen: Läs fler böcker. Läs tidningar. Läs böcker som du tycler är kul. Läs könlitteratur. Läs fackböcker.
 Man ska alltså räkna ut volymen av den här figuren som jag har ritat, och därefter räkna ut hur många människor som rymmer i polen. Det är som en cylinder. Men jag undrar hur man räknar ut volymen av cylinder när man har som en ”tjocklek” runt cylindern
Man ska alltså räkna ut volymen av den här figuren som jag har ritat, och därefter räkna ut hur många människor som rymmer i polen. Det är som en cylinder. Men jag undrar hur man räknar ut volymen av cylinder när man har som en ”tjocklek” runt cylindern
Är det a-uppgiften elelr b-uppgiften du räknar på? Till a-uppgiften behäver du inte 0,06 m alls, bara 1,18 m. Toll b-uppgiften behöver du inte 1,18 m alls, bara 0,06 m. Läsförståelse!
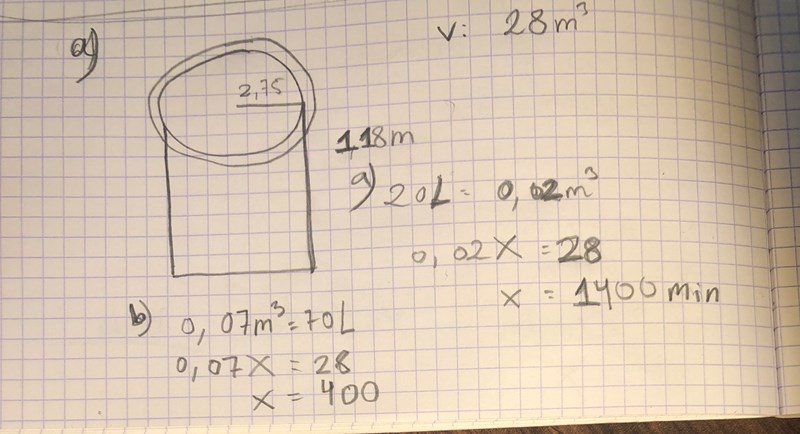
 B uppgiften är den jag nu försöker lösa. Det är ju volymen man ska räkna ut av en cylinder. V=B*h
B uppgiften är den jag nu försöker lösa. Det är ju volymen man ska räkna ut av en cylinder. V=B*h
Kommer inte vidare?
jag tänker att 0,06 ska ritas utifrån.
Jag tror man ska lösa uppgiften såhär :
vi vill ta reda på volymen, då behöver vi inte veta volymen av det som är utanför poolen (0,06m). Därför beräknar jag volymen som följande :
2,75^2*pi*1,18=28m^3
nu vet jag att volymen är 28m^3
vi vet att en person rymmer 0,07m^3
x är max antalpersoner
0,07x=28
...svaret jag får x=400
I det här fallet är det smart att räkna i enheten dm, eftersom en kubikdecimeter är precis samma sak som en liter och vi vet att en människa har volymen 70 liter. Hur stor är poolens radie, mätt i dm? Hur mycket är 0,06 m, mätt i dm? Du har skrivit att volymen är basytan gånger höjden. Basytan är en cirkel. Hur beräknar man arean av en cirkel (repetition)?
Man tar radien^2*pi för cirkelnsarea men nu har vi även en höjd och vill beräkna volymen så vi tar r^2*pi*h
På b frågar man hur många hur många måste vara i poolen för att den ska börja rinna, vi vet att poolen rymmer totalt 400personer med volymen 0,07m^3. X är totalt antal pers som rymmer i poolen
Renny19900 skrev:
Man ska alltså räkna ut volymen av den här figuren som jag har ritat, och därefter räkna ut hur många människor som rymmer i polen. Det är som en cylinder. Men jag undrar hur man räknar ut volymen av cylinder när man har som en ”tjocklek” runt cylindern
Vad menar du med "tjocklek runt cylindern"?
Du har fått veta det flera gånger redan: du ska inte fylla poolen med människor. Den är nästan full med vatten, och du ska ta reda på hur många människor som behöver gå i för att vattnet ska börja rinna över.
Jaha ok, isåfall
402*0,07= Ca 28,14m^3 (2 personer mer)
403*0,07=28,21..m^3
jag tror att jag har gjort fel i A uppgiften därför blir det fel i B. Volymen ska inte vara 28m^3 om svaret ska vara att 20 personer mer (det står så i facit)
Jag menar det som är runt cirkeln och som motsvarar 0,06m ser ut som en tjocklek
Räkna ut volumen för en cirkulär skiva med samma radie som poolen och tjockleken 6 cm. Sedan skall du ta reda på hur många människor som behöver kliva ner i poolen för att vattenytan skall höjas så mycket.
Om volymen till exempel vore 210 liter (påhittat värde), så skulle det motsvara 211/70 = 3 personer.
Ta det mest cylindriska glas du har hemma. Fyll det helt med vatten. Häll ut lite.
Så ser det ut.
Smaragdalena skrev:Räkna ut volumen för en cirkulär skiva med samma radie som poolen och tjockleken 6 cm. Sedan skall du ta reda på hur många människor som behöver kliva ner i poolen för att vattenytan skall höjas så mycket.
Om volymen till exempel vore 210 liter (påhittat värde), så skulle det motsvara 211/70 = 3 personer.
Cirkulära skivans volym skulle bli : 6m*2,75^2*pi=1,42m^3. Jag vet att man sen ska ta 0,07x=1,42
x=20
men jag förstår inte varför man bara ska räkna ut volymen av den cirkuläraskivan ovan och inte hela poolen, varför blir det fel när jag räknar ut hela volymen 28m^3 sen tar 0,07x=28
x=400 som rymmer i poolen, om det kommer 1 som hoppar in i poolen börjar vattnet rinna
Smaragdalena skrev:Räkna ut volumen för en cirkulär skiva med samma radie som poolen och tjockleken 6 cm. Sedan skall du ta reda på hur många människor osom behöver kliva ner i poolen för att vattenytan skall höjas så mycket.
Om volymen till exempel vore 210 liter (påhittat värde), så skulle det motsvara 211/70 = 3 personer.
Om volymen är 1,18*2,75^2*pi =28m^3=28 000L. Varför kan man inte dela på 70? Snälla någon som kan förklara.
Jag förstår inte varför man bara ska räkna ut volymen för cirkelskivan och därefter dividera på 0,07m^3?
Jag ber om ursäkt för att jag inte förstår... :(((
Renny19900 skrev:Smaragdalena skrev:Räkna ut volumen för en cirkulär skiva med samma radie som poolen och tjockleken 6 cm. Sedan skall du ta reda på hur många människor osom behöver kliva ner i poolen för att vattenytan skall höjas så mycket.
Om volymen till exempel vore 210 liter (påhittat värde), så skulle det motsvara 211/70 = 3 personer.
Om volymen är 1,18*2,75^2*pi =28m^3=28 000L. Varför kan man inte dela på 70? Snälla någon som kan förklara.
Jag förstår inte varför man bara ska räkna ut volymen för cirkelskivan och därefter dividera på 0,07m^3?
Jag ber om ursäkt för att jag inte förstår... :(((
Du behöver inte be om ursäkt.
Det här är lite knepigt om man inte får tankarna in på rätt banor.
Poolen är inte helt fylld. Ovanför vattenytan finns en cylinder av luft som har samma bottenarea som poolen men som bara är 0.06 meter hög.
"Luftcylindern" har volymen .
Varje person har en volym som är liter, dvs .
Om x personer sjunker ner under vattenytan så kommer de att tränga undan vatten.
När denna undanträngda volym är lika stor som "luftcylinderns" volym så börjar vattnet rinna ut över poolkanten.
Detta ger dig ekvationen
Hämta ett glas. Fyll det med vatten nästan upp till kanten. Detta motsvarar poolen innan någon har klivit ner i den. Lägg ner en sten (eller något annat tungt) i vattenglaset. Lägg i en till, och en till, och en till, tills vattnet rinner över. Detta motsvarar när fler och fler människor kliver ner i vattnet.
Yngve skrev:Renny19900 skrev:Smaragdalena skrev:Räkna ut volumen för en cirkulär skiva med samma radie som poolen och tjockleken 6 cm. Sedan skall du ta reda på hur många människor osom behöver kliva ner i poolen för att vattenytan skall höjas så mycket.
Om volymen till exempel vore 210 liter (påhittat värde), så skulle det motsvara 211/70 = 3 personer.
Om volymen är 1,18*2,75^2*pi =28m^3=28 000L. Varför kan man inte dela på 70? Snälla någon som kan förklara.
Jag förstår inte varför man bara ska räkna ut volymen för cirkelskivan och därefter dividera på 0,07m^3?
Jag ber om ursäkt för att jag inte förstår... :(((
Du behöver inte be om ursäkt.
Det här är lite knepigt om man inte får tankarna in på rätt banor.
Poolen är inte helt fylld. Ovanför vattenytan finns en cylinder av luft som har samma bottenarea som poolen men som bara är 0.06 meter hög.
"Luftcylindern" har volymen .
Varje person har en volym som är liter, dvs .
Om x personer sjunker ner under vattenytan så kommer de att tränga undan vatten.
När denna undanträngda volym är lika stor som "luftcylinderns" volym så börjar vattnet rinna ut över poolkanten.
Detta ger dig ekvationen
Man ska alltså inte räkna med antalet personer som är längst nere i poolen utan man ska bara räkna med antalet som ligger i cirkelskivan.
Man ska bara räkna med antalet som är nedtryckta i cirkelskivan..
isåfall blir svaret :
0,07x=1,425
x=Ca 20personer. Jag förstår nu. Men borde man ine svara när det är fler än 20personer i poolen?
Ang fråga A) så tänkte jag så här : V =28m^3
0,04x=28
x=700min
Renny19900 skrev:
Man ska alltså inte räkna med antalet personer som är längst nere i poolen utan man ska bara räkna med antalet som ligger i cirkelskivan.
Man ska bara räkna med antalet som är nedtryckta i cirkelskivan..
isåfall blir svaret :
0,07x=1,425
x=Ca 20personer. Jag förstår nu. Men borde man ine svara när det är fler än 20personer i poolen?
Ang fråga A) så tänkte jag så här : V =28m^3
0,04x=28
x=700min
Det spelar ingen roll var i poolen människorna ligger, så länge de är helt nedsänkta under vattenytan.
Ja svaret ska vara 21 personer. 20 personer får plats utan att vattnet rinner över.
---------
På a-uppgiften gäller att poolen rymmer ungefär 28.03 m^3 vatten.
Slangarna fyller tillsammans poolen med 2*20 = 40 liter per minut, vilket motsvarar 0.04 m^3 per minut.
Att fylla poolen tar då x minuter, där x fås ur ekvationen 28.03 = 0.04*x, dvs x är ungefär lika med 701 minuter. Detta motsvarar 11 timmar och 41 minuter.
Svaret blir alltså ungefär 12 timmar.




