Corioliskrafter
Vid härledning av fiktiva krafter är sista steget:
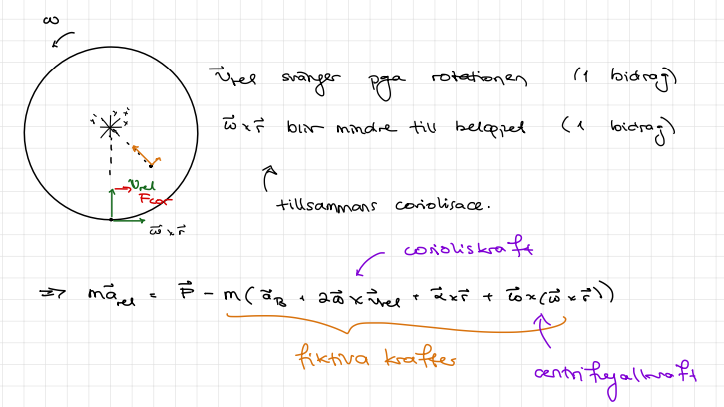
Alltså att man har den härledda kraften och så löser man ut . Sedan blir alltid alltid 0 när man sedan räknar på det i uppgifter, varför? Vad är egentligen F för kraft här?
Det är den ”vanliga” kraften som du har i den vanliga formen av Newtons ekvationer (dvs i ett inertialsystem).
F = ma, där a är accelerationen relativt ett inertialsystem.
Aa, jag tror jag förstår. Det är den enda ”verkliga” kraften här. Om jag trycker på en låda ger jag den kraften , men om den råkar vara i ett roterande system kommer alla dessa andra krafter också ”synas” om man zoomar ut tillräckligt.
Stämmer det?
Vad menar du med att krafter syns när man zoomar ut?
När jag släpper en boll på Jorden så blir ju den framförallt påverkad av en gravitationskraft. Men den blir också påverkad av en kraft från solen och Vintergatans mittpunkt osv. Lite samma resonemang som när jag säger att jag åker i 30 km/h och inte 30 + jordens hastighet.



