Cosinusekvation

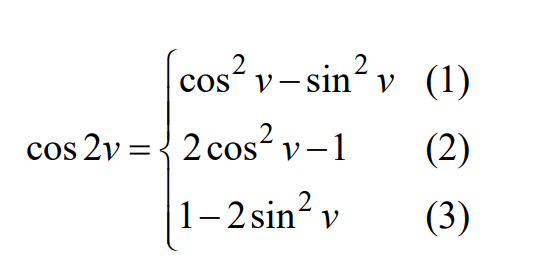
Så här har jag läst den

Två små kommentarer:

• cos(x)=0 har perioden π
• cos(x)=1/2 har även en lösning om du går π/3 medsols i enhetscirkeln 

Sictransit råkade skriva "plusminus" på fel ställe.

(Plusminus pi/3)+ (n*2pi)

Den första lösningen kan man också se som 

(Plusminus pi/2)+ (n*2pi)

sictransit skrev:

Två små kommentarer:

• cos(x)=0 har perioden π
• cos(x)=1/2 har även en lösning om du går π/3 medsols i enhetscirkeln 

 

Har du en bild på enhetscrikeln som du skulle kunna markera. Jag har svårt att förstå varför $\cos \left(x\right)=0$har perioden $\mathrm{\pi }.$

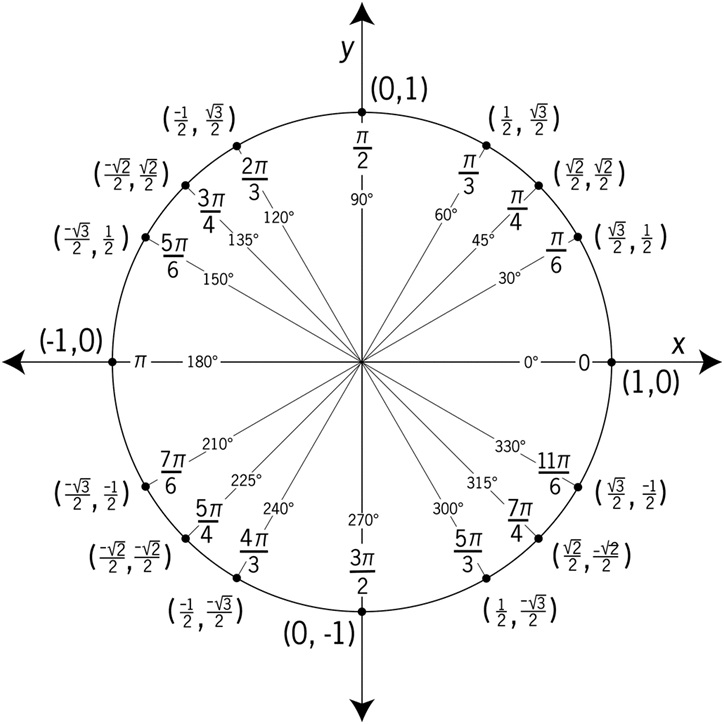
Leta fram enhetscirkeln. Jag har postat den tidigare i dina trådar. Annars är den en googling bort. Cosinus har värdet noll ”klockan 12” och ”klockan 6”, alltså rakt upp och rakt ned. Mellan dessa är det 180 grader eller pi radianer. 

Snyggt. Ser du då på den att cosinusvärdet är 0 vid vinklarna 90° + n•180° ($\frac{\pi}{2}+n\cdot\pi$ radianer)?

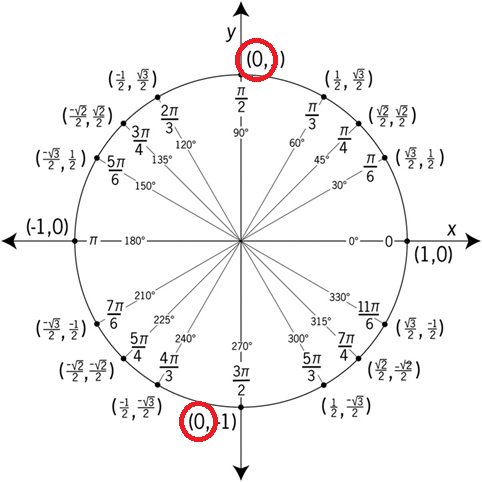
Yngve skrev:

Snyggt. Ser du då på den att cosinusvärdet är 0 vid vinklarna 90° + n•180° ($\frac{\pi}{2}+n\cdot\pi$ radianer)?

Nja, skulle du kunna markera. Där jag ska titta ?

Arup skrev:

Nja, skulle du kunna markera. Där jag ska titta ?

Viktig basfakta om enhetscirkeln: En punkt på en enhetscirkel har koordinaterna (cos(v), sin(v)).

Den horisontella koordinaten är alltså lika med cos(v) och den vertikala koordinaten är lika med sin(v).

Eftersom den horisontella koordinaten är lika med 0 "klockan 12" (dvs då vinkeln är 90°+n•360°) och "klockan 6" (dvs då vinkeln är 180°+n•360°) så innebär det att cosinusvärdet är lika med 0 då vinkeln antingen är 90°+n•360° eller 180°+n•360°.

Dessa vinklar kan enklare skrivas 90°+n•180° (eller $\frac{\pi}{2}+n\cdot\pi$ radianer).