de Moivres formel, komplexa tal

Är du säker på att argumentet skall vara $45^\circ$? Vilken kvadrant är du då i? Vilken kvadrant ligger $i-1$ i?

AlvinB skrev:

Är du säker på att argumentet skall vara $45^\circ$? Vilken kvadrant är du då i? Vilken kvadrant ligger $i-1$ i?

Oj, borde det inte vara 135 då? 1-i ligger väl i andra kvadranten?

Jag antar att du menar $i-1$ och inte $1-i$. I så fall har du helt rätt, $135^\circ$ är korrekt.

Utöver det som AlvinB redan påpekat så bör du använda exakta värden så långt det går.

Till exempel absolutbeloppet bör du skriva som $2\sqrt{2}$.

Leta sedan i ditt formelblad efter exakta cosinus- och sinusvärden för argumentet.

När man multiplicerar tre komplexa tal (z*z*z) multiplicerar man deras belopp och summerar deras vinklar.

$z*z*z=(\sqrt{2}{)}^3\angle 3*{135}^{°}=2\sqrt{2}\angle {405}^{°}=2\sqrt{2}\angle {405}^{°}-{360}^{°}=2\sqrt{2}\angle {45}^{°}$ 

Hej om jag förstod era kommentarer rätt, har jag tänkt rätt med den här uträkningen?

Mvh 

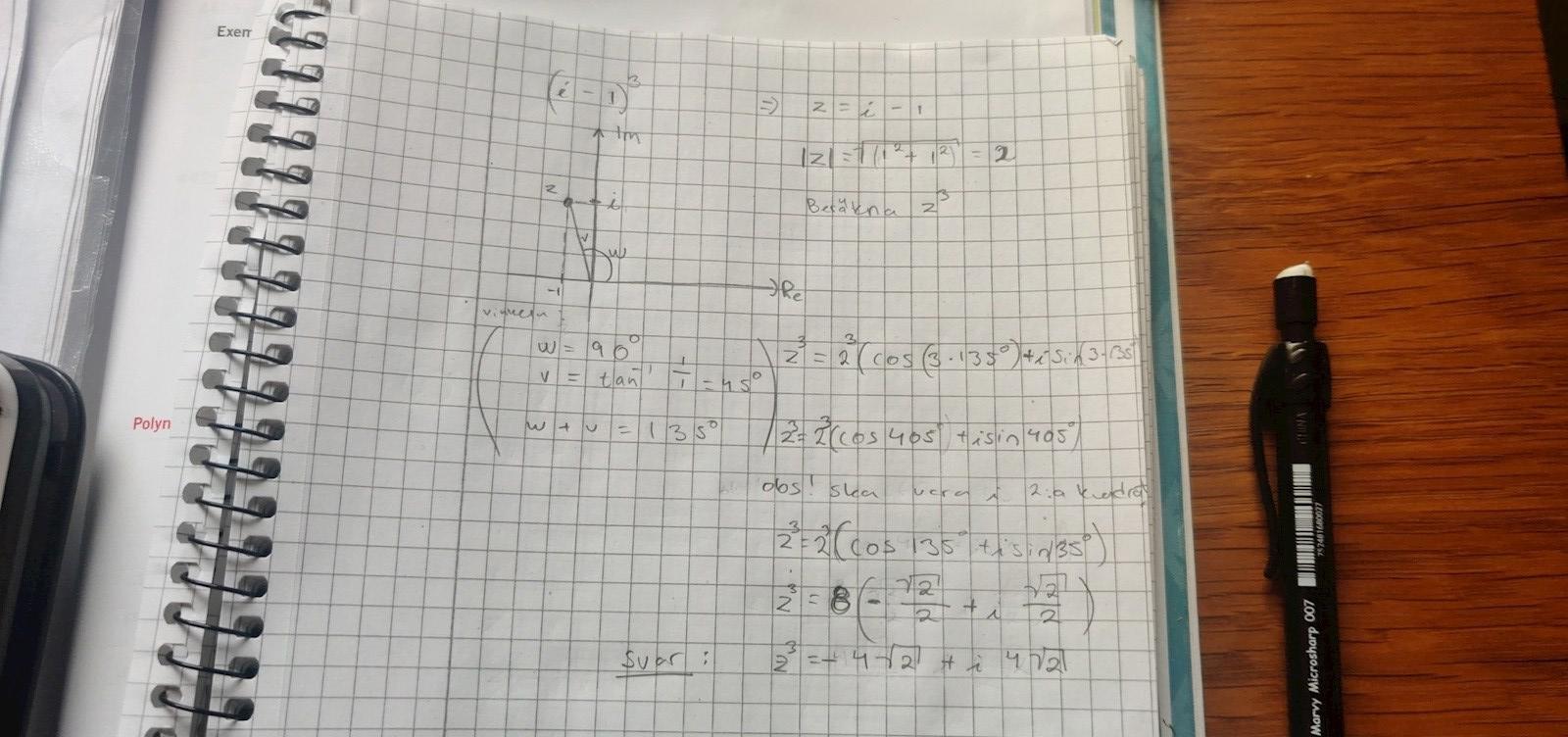
Nej det stämmer inte.

Skapa en ny tråd med din uträkning så får du både snabbare och bättre svar.