Definiera h(x) för x=4 så att h(x) blir kontinuerlig för alla x

En funktion är kontinuerlig för om den är definierad utan ”hack”, dvs att hela kurvan hänger ihop. En kurva som ser ut såhär: 

är exempelvis inte kontinuerlig. 

Din funktion har ett hål då x är lika med 4. Funktionen är helt enkelt inte definierad där, då division med noll uppstår.

För att funktionen ska vara definierad då x är 4, kan vi därför specificera att funktionen i den punkten har ett specifikt värde. Vi kan välja vilket värde som helst, men om vi väljer ett värde som gör att kurvan ser ut såhär: 

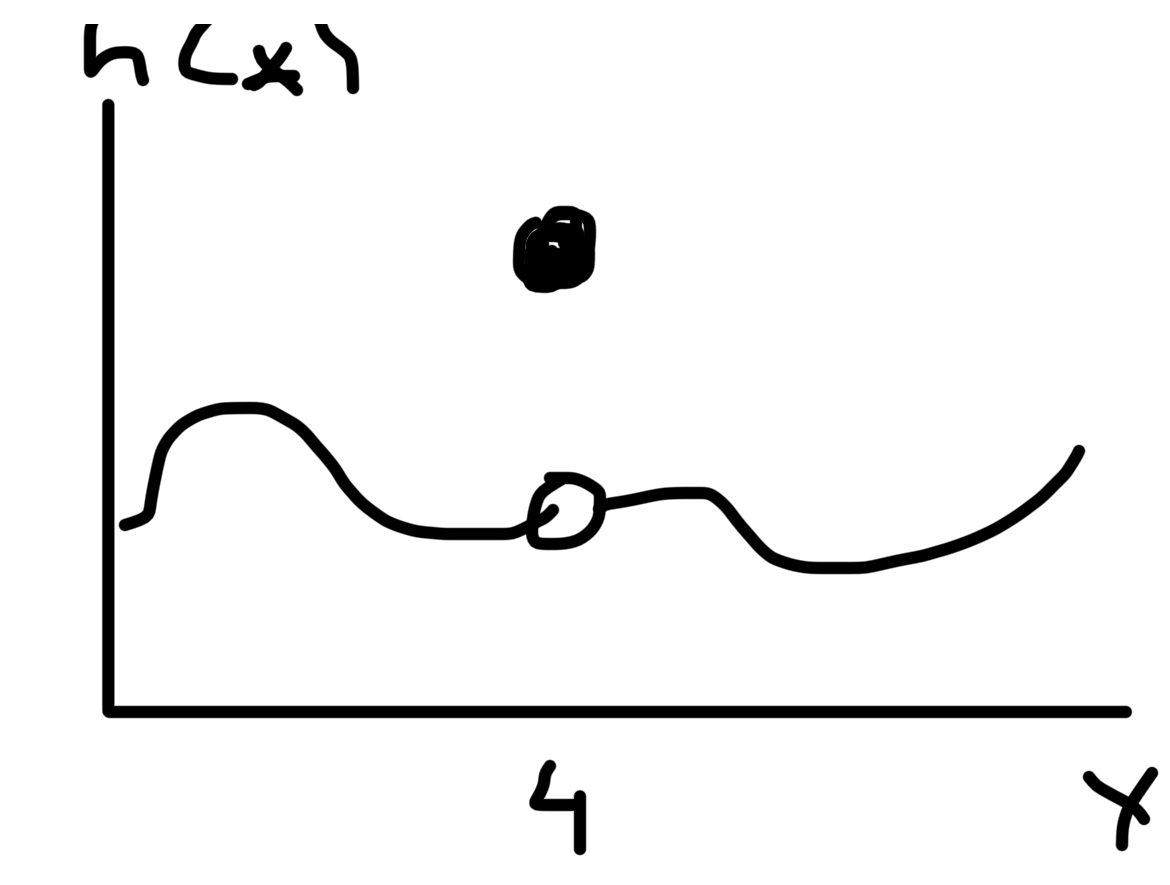är funktionen inte kontinuerlig. Vilket värde ska vi välja på h(4) så att hela kurvan blir sammanhängande? :)

Smutstvätt skrev:

En funktion är kontinuerlig för om den är definierad utan ”hack”, dvs att hela kurvan hänger ihop. En kurva som ser ut såhär: 

är exempelvis inte kontinuerlig. 

Din funktion har ett hål då x är lika med 4. Funktionen är helt enkelt inte definierad där, då division med noll uppstår.

För att funktionen ska vara definierad då x är 4, kan vi därför specificera att funktionen i den punkten har ett specifikt värde. Vi kan välja vilket värde som helst, men om vi väljer ett värde som gör att kurvan ser ut såhär: 

är funktionen inte kontinuerlig. Vilket värde ska vi välja på h(4) så att hela kurvan blir sammanhängande? :)

Tusen tack!

1. Jag har sett detta i boken också. En vit prick är alltså ”ej inkluderande?

2. Känns som att jag går emot matematiska axiom hela tiden ju längre jag kommer. Så jag ”får” alltså introducera en funktion inom en funktion som här?

då förstår jag!

..Och är det alltså tänkt att jag får använda ett digitalt verktyg här? Eller ska jag testa mig fram och uppskatta deltan?

Grafiskt:

1. Jag har sett detta i boken också. En vit prick är alltså ”ej inkluderande?

Ja, ihålig betyder inte ingår, ifylld betyder ingår.

Känns som att jag går emot matematiska axiom hela tiden ju längre jag kommer. Så jag ”får” alltså introducera en funktion inom en funktion som här?

Det är inte två olika funktioner, det är två uttryck som beskriver en och samma funktion. De olika uttrycken talar om för oss vad funktionen ska göra med $x$, beroende på vilket värde $x$ har. 

De flesta funktioner man stöter på är trevliga på det sättet att de är definierade med en enda formel som talar om vilket värde vi får ut för varje värde vi stoppar in. Men en funktion mer generellt är ett objekt som för varje värde i någon definitionsmängd tilldelar ett värde ur någon värdemängd. Exempelvis kan jag definiera en funktion från $\{1,2,3\}$ till $\{a,b,c\}$ genom att beskriva vad funktionen antar för värde för varje input: $f(1)=c$, $f(2)=a$ och $f(3)=a$.

Jag kan även definiera funktionen genom att skriva

$f(x)=a\quad\text{om}\quad x\neq 1$

$f(x)=c\quad \text{om}\quad x=1.$

Dessa instruktioner talar om för oss vad funktionen gör med samtliga inputs från sin definitionsmängd, och är därför en giltig definition.

Här är vår definitionsmängd bara tre olika tal, men ofta har funktioner en oändlig definitionsmängd, t.ex. alla reella tal, eller alla reella tal utom något enstaka.

När man endast säger att t.ex. "$f(x)=\frac{5}{x-2}$" så brukar man mena att definitionsmängden för $f$ är alla reella tal för vilket uttrycket är definierat, dvs. alla reella tal utom talet 2. Vi kan därför om vi vill definiera en funktion definierad för alla reella tal som har värdet $\frac{5}{x-2}$ för alla reella tal $x$ utom 2, och $f(2)=37$. Vi har helt enkelt utökat funktionen $f$ med ytterligare ett möjligt värde.

..Och är det alltså tänkt att jag får använda ett digitalt verktyg här? Eller ska jag testa mig fram och uppskatta deltan?

Jag tror tanken är att uttrycket för funktionen för $x\neq 4$ kan förkortas till $\frac{x}{2}$ då både täljare och nämnare innehåller en faktor $x-4$. Då blir det lite lättare att skissa funktionen om du väljer att göra det.

Gustor skrev:

1. Jag har sett detta i boken också. En vit prick är alltså ”ej inkluderande?

Ja, ihålig betyder inte ingår, ifylld betyder ingår.

Känns som att jag går emot matematiska axiom hela tiden ju längre jag kommer. Så jag ”får” alltså introducera en funktion inom en funktion som här?

Det är inte två olika funktioner, det är två uttryck som beskriver en och samma funktion. De olika uttrycken talar om för oss vad funktionen ska göra med $x$, beroende på vilket värde $x$ har. …

 

Tack. Lite som det jag lärde mig under programmeringen när vi gick igenom ”Data Science” och relationen mellan oberoende och beroende variabel. Nu klickar det!

”Jag tror tanken är att uttrycket för funktionen för x≠4 kan förkortas till x2 då både täljare och nämnare innehåller en faktor x-4. Då blir det lite lättare att skissa funktionen om du väljer att göra det.”

smart! Ser det nu; såg bara inte faktorerna först.