Definition av funktion
Vad är definitionen av begreppet funktion?
I flera böcker står något som: "varje invärde ger exakt ett utvärde"
Detta förklarar t.ex varför y2=x inte räknas som en funktion (av x).
Vad med y=1/x ? Där brukar man säga att det är en funktion där domänen är alla reella x utom x=0
Så, kan man då skriva en funktion (genom att begränsa domänen/subdomänen) som ger följande graf:
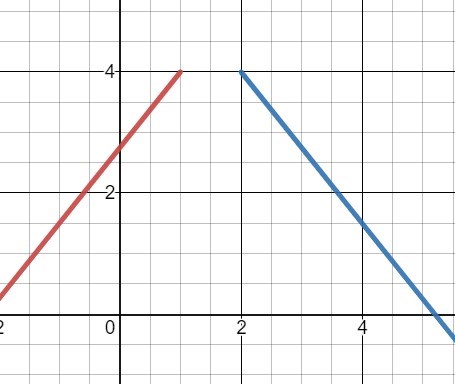
(Ni får tänka er att den röda och blå delen har samma färg och att linjerna fortsätter utanför rutan.)
Detta är ett riktigt exempel från en bok där man skall svara om detta är en funktion eller inte.
Vad jag minns från envariabeln så är definitionen av en funktionen sådan att . Om vi låter och så är det inte en funktion därför att för x=0 får vi inte tillbaka något y-värde eftersom den är odef där men om vi istället låter {} så är det en funktion. Med det sagt vill jag tro att om du justerar domänen/kodämen så kan du säga att det är en funktion men om så är det inte det.
Jag vet inte om jag svarar på din fråga, är inte helt säker själv så ta mitt svar med en stor nypa salt. Intressant fråga dock!
Jag tycker att det här sammanfattar funktionsbegreppet bra, speciellt avsnittet "definition".
Yngve skrev:Jag tycker att det här sammanfattar funktionsbegreppet bra, speciellt avsnittet "definition".
Räknas "går mot oändligheten" som ett element? ex. f(x)=1/x
Hur är det med grafen, kan det vara en funktion och hur skulle den kunna se ut?
joculator skrev:
Räknas "går mot oändligheten" som ett element? ex. f(x)=1/x
Jag förstår nog inte riktigt vad du menar här.
Om vi t.ex. väljer att definitionsmängden där ska vara alla reella tal som är större än 0 så blir även värdemängden alla reella tal som är större än 0.
Både definitions- och värdemängden har då oändligt många element som alla är reella tal.
Vad gäller grafen så tycker jag att det ser ut som om den skulle kunna representera följande funktion:
f(x)=-1,25|x-1,5|+4,625, med definitionsmängd "alla reella tal x förutom 1 < x < 2" (eller om ändpunkterna inte ska vara med).
1. Detta är pedagogiskt sett kanske inte den rätta platsen för DEN STRIKTA definitionen av en funktion , som lyder: f är en funktion av A in i B omm f är en delmängd av den Cartesiska produkten A x B (=mängden av par (a,b) där a tillhör A och b tillhör B) sådan att om både (a,b) och (a,b1 ) tillhör f så är b=b1 Jag nämner den här enbart för att varje pedagogiskt bra förklaring jag sett lämnar frågor av den typ som frågeställaren ställer.
2. Ang frågan om oändligheten: R innehåller INTE oändligheten. Man kan adjungera elementet oändligheten och på så sätt utvidga R, men då är det inte längre R. (En välkänd representation av oändligheten går till så här: Ställ en cirkel ovanpå och tangerande den reella axeln, så kommer linjen mellan "nordpolen" på denna cirkel och vilket reellt tal som helst att råka cirkeln någonstans. Dessa skärningspunkter motsvarar då alla reella tal och nordpolen själv motsvarar oändligheten.)
'definitionen' i boken är:
"Om vi skickar in samma tal in till 'funktionsmaskinen' får vi ut samma tal varje gång"
(detta är min översättning och på originalspråket är det tydligt att utgående 'tal' är i singular)
Några av bokens exempel var grafer som visar:
a) f(x)=1/x
b) y^2+x^2=10
c) y^3-2y=x
d) grafen jag postat ovan
Med bokens definition blir det egentligen en enkel uppgift ...
Målgruppen för boken är 12-åringar. Jag hjälper ibland en 'studiegrupp' som inte pratar svenska.
Vi använde denna fördjupningsuppgift för att de skulle få se Pluggakuten (och såklart för att få svar).
De har inga egna konton på PA. En stor orsak till det är språk och en liten orsak är avsaknad av svenska personnummer.
Alla frågor är deras frågor (översatta av mig).
Jag postade i Matte 2 eftersom Matteboken.se inte riktigt har så 'avancerade' grafer som exempel på funktioner (i åk7 och åk9) så Matte 2 kändes rätt.
Tack alla. Mycket hjälpsamt. Eleverna tycker att PA är 'coolt' och att de fick bra svar.
Edit: Boken är för 14-åringar, det är just de här eleverna som är 12.




