definitionsmängd
Hej!
Min mattelärare har sagt att till alla funktioner man skriver MÅSTE man ange definitionsmängd. JAg har kommit fram till en korrekt funktion till nedanstående fråga, men har lite svårt att veta hur jag ska komma fram till definitionsmängden. Det enda jag kan tänka på är att 0<s, men vet inte hur jag ska tänka för att veta hur stort s kan som möjligast vara. är det 0<s<80?
Funktionen var V(s)=(40-s^3)/2

Extrema konstruktioner är ett rätblock med nästan h=0 vilket ger 2s^2=80 dvs. s<SQRT(40).
Alltså har vi att
0<s<SQRT(40)
Din formel verkar ej vara rätt
Begränsningsarea: 80 = 2s^2 + 4hs vilket ger
h=(40 - s^2)/(2 s)
Volymen
V(s) = s^2 h = (1/2) s (s^2-40)
Ritar vi denna får vi en väldefinierad graf
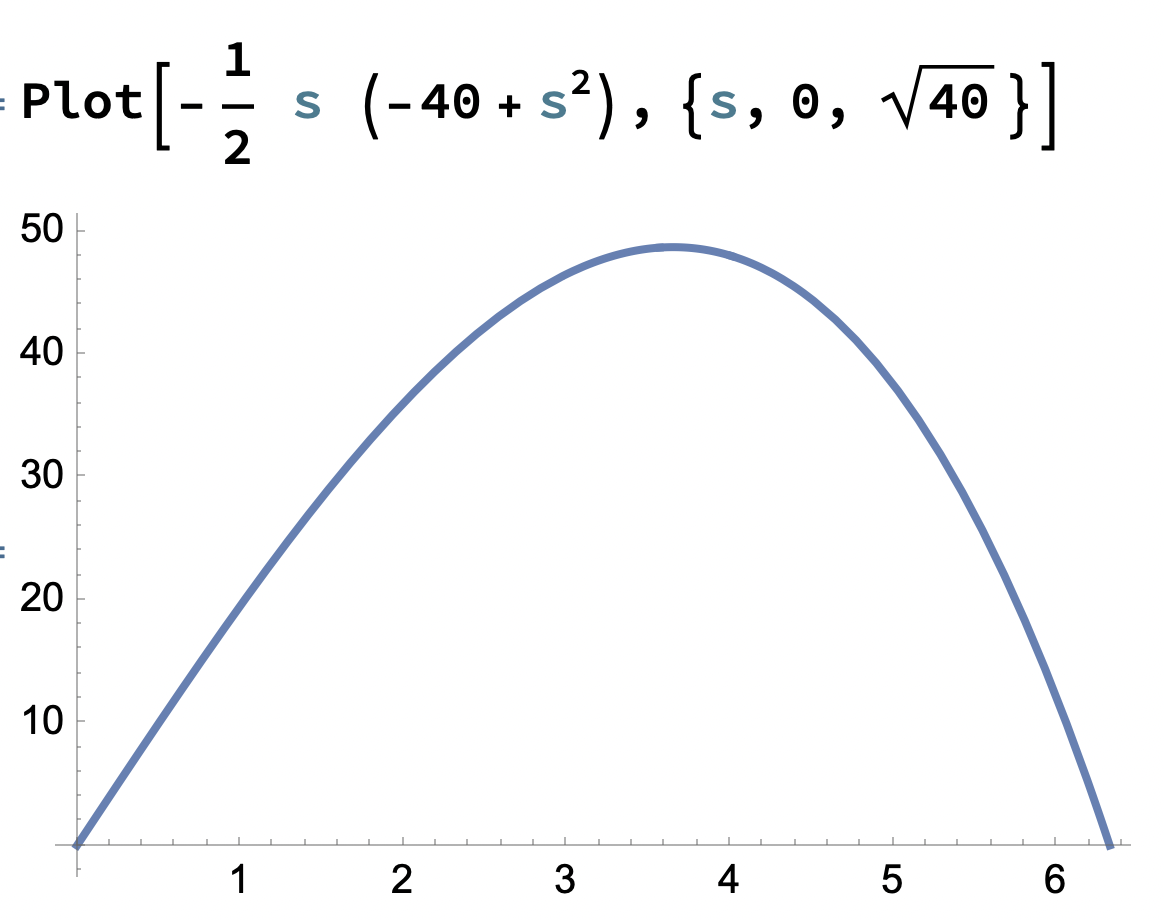
Att sedan din lärare säger att man MÅSTE är rent trams. Det underlättar senare beslut (om t.ex. en lösning ligger i def. internvallet etc.) men hen kanske skall ta och kontakta Natur och Kultur eller de andra för 99% av alla uppgifter saknar def. intervall. Det är dessutom så illa att de ritar sina grafer som jag ovan där ändpunkterna eg. skall vara tomma cirklar för att indikera det öppna intervallet.
Men, gör som hen säger, annars drar hen med glädje 1p på proven för dig… I bland är kejsaren(-innan) fullt påklädd... iaf. betraktat från en politisk synvinkel…

Här är screenshot på facit, såvida inte jag skrev något slarvigt så har jag skrivit samma. Hur tänkte du när du löste denna uppgift? Kan vara så att det är fel i facit oxå.
hur fick du andra delen av intervallet (SQRT(40))? hängde inte helt med där.
Och japp, du har helt rätt, hon gör mer än gärna poängavdrag om man inte har med definitionsmängd i en funktion. Fick själv avdrag för att jag inte skrev definitionsmängd på en uppgift för att det brister i kommunikationen. Hade skrivit definitionsmängd på alla andra uppgifter där jag skulle skapa funktioner, men just den jag skulle gjort det på missade jag det.
Men det är lite besides the point. hur fick du SQRT(40)?

är inte samma sak om facit. Facit är samma sak som min
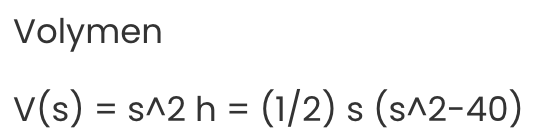
Om man låter figuren urarta mot sina extrema dimensioner har vi en höjd = 0 (nära 0) och då är begränsningsytan = 2 kvadrater (topp och botten)
2s*2 = 80
s^2=40
s=SQRT(40)
Alltså är s<sqrt(40).
Det kan inte vara s≤SQRT(40) för det innebär att h=0 då s=40. Man får tänka sig en oändligt liten höjd, därför blir det "<"-tecken.
(Vissa) Lärare är besynnerliga.
ja, det är ändå helt logsikt att tänka så, tack för hjälpen!
KlmJan skrev:ja, det är ändå helt logsikt att tänka så, tack för hjälpen!
Här är en liten "Mathematica-lösning". Notera att man även kan ställa kravet h>0 vilket ger 0<s<2aqrt(10)


tack!


