Definitionsmängd och målmängd

Vad är f(x) och g(x)?

Inabsurdum skrev:

Vad är f(x) och g(x)?

 :)

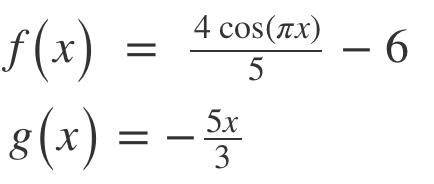g(x) är rätt. f(x) har då definitionsmängd R. Målmängd är egentligen en definitionsfråga, om det är värdemängd som menas (https://sv.wikipedia.org/wiki/M%C3%A5lm%C3%A4ngd) så är det inte $[-11, \infty]$, tänk på att värdemängd för $\cos{x}$ (och $\cos{\pi x}$) är $[-1,1]$.

Inabsurdum skrev:

g(x) är rätt. f(x) har då definitionsmängd R. Målmängd är egentligen en definitionsfråga, om det är värdemängd som menas (https://sv.wikipedia.org/wiki/M%C3%A5lm%C3%A4ngd) så är det inte $[-11, \infty]$, tänk på att värdemängd för $\cos{x}$ (och $\cos{\pi x}$) är $[-1,1]$.

Nej precis värdemängden har jag räknat fram till att det är värdena från h(1) till h(6), därefter upprepar sig värdena igen. Ex: h(1) = $-\frac{28}{5}$, h(2)=$-\frac{32}{5}$..... h(6)=$-\frac{26}{5}$, därefter så upprepar de sig igen som nämnt -> h(7)=$-\frac{28}{5}$.

Men det är just målmängden som jag är ute efter, det borde ju vara [−11,∞[?

Varför tar du bara heltal (h(1), h(2), ...))? Och hur kommer du fram till $[-11, \infty)$? Kan du posta hela frågan?

Inabsurdum skrev:

Varför tar du bara heltal (h(1), h(2), ...))? Och hur kommer du fram till $[-11, \infty)$? Kan du posta hela frågan?

Det är ganska många frågor i uppgiften men jag visar hela så kanske det klargör mer:

Jaha ja då är definitionsmängd och målmängd som du skrev, svårt utan definition av f! :-)

Men när du räknar på värdemängden kan du inte bara räkna på heltal.

Inabsurdum skrev:

Jaha ja då är definitionsmängd och målmängd som du skrev, svårt utan definition av f! :-)

Men när du räknar på värdemängden kan du inte bara räkna på heltal.

Va bra! :D

Oj ok, ska jag då även testa med halvtal? Alltså 0.5, 1.5..? Antog att det räckte med att räkna med heltal eftersom det är en periodiskfunktion (hoppas jag). 

Den är periodisk men uppnår inte max/min vid heltal: $\cos{(\pi x)}$ uppnår min/max vid 1,2,... men $\cos{(-\frac{5}{3}\pi x)}$ gör det inte. Testa att plotta funktionerna. Men värdet kommer alltid att vara i $[-1,1]$, det kan man använda för att bestämma värdemängden.

Inabsurdum skrev:

Den är periodisk men uppnår inte max/min vid heltal: $\cos{(\pi x)}$ uppnår min/max vid 1,2,... men $\cos{(-\frac{5}{3}\pi x)}$ gör det inte. Testa att plotta funktionerna. Men värdet kommer alltid att vara i $[-1,1]$, det kan man använda för att bestämma värdemängden.

Jaha ok, jag får tänka om där, tack så mycket för din hjälp! :D

Inabsurdum skrev:

Den är periodisk men uppnår inte max/min vid heltal: $\cos{(\pi x)}$ uppnår min/max vid 1,2,... men $\cos{(-\frac{5}{3}\pi x)}$ gör det inte. Testa att plotta funktionerna. Men värdet kommer alltid att vara i $[-1,1]$, det kan man använda för att bestämma värdemängden.

Hej igen ! Jag vet inte riktigt om jag ska skriva ett nytt inlägg men testar att citera härifrån.

Du hade självklart rätt att mitt värdemängd som jag trodde jag hade va fel, när jag plottar ditt $\cos{(-\frac{5}{3}\pi x)}$ så är värdet mellan $[-1,1]$, vilket är rätt, hur fick du fram detta cos funktion? Och varför kan jag inte använda mitt "orginala" cos funktion alltså h(x)= $\frac{4}{5}\cos \left(\frac{5\pi x}{3}\right)-6$

Cos kommer alltid att ha värden mellan -1 och 1 oavsett vad man stoppar in i argumentet. Det är bra att veta t.ex. när man jobbar med gränsvärden, då det är användbart att veta att cos alltid är begränsad. Sen kan det vara så att $cos(g(x))$ inte alltid uppnår alla värden mellan -1 och 1 om värdemängden för $g(x)$ är "för liten", men speciellt om man vet att värdemängden är hela $\mathbb{R}$ som för $-\frac{5}{3}\pi x$ så kommer $\cos{(-\frac{5}{3}\pi x)}$ att ha min -1 och max 1.

Så sen är det bara att kolla att om hela $\cos{(-\frac{5}{3}\pi x)}$ delen kan bli min -1 då blir $h(x)$ som minst $\frac{4}{5}\cdot (-1) - 6 = -\frac{34}{5}$ och som mest $\frac{4}{5}\cdot 1 - 6 = -\frac{26}{5}$.

Inabsurdum skrev:

Cos kommer alltid att ha värden mellan -1 och 1 oavsett vad man stoppar in i argumentet. Det är bra att veta t.ex. när man jobbar med gränsvärden, då det är användbart att veta att cos alltid är begränsad. Sen kan det vara så att $cos(g(x))$ inte alltid uppnår alla värden mellan -1 och 1 om värdemängden för $g(x)$ är "för liten", men speciellt om man vet att värdemängden är hela $\mathbb{R}$ som för $-\frac{5}{3}\pi x$ så kommer $\cos{(-\frac{5}{3}\pi x)}$ att ha min -1 och max 1.

Så sen är det bara att kolla att om hela $\cos{(-\frac{5}{3}\pi x)}$ delen kan bli min -1 då blir $h(x)$ som minst $\frac{4}{5}\cdot (-1) - 6 = -\frac{34}{5}$ och som mest $\frac{4}{5}\cdot 1 - 6 = -\frac{26}{5}$.

Nu vart jag lite mer osäkert, för det är h(x) värdemängd jag ska bestämma eller hur så jag svarade i uppgiften:

Då fick jag feedback från en mentor att:

Men mitt största och minsta värde är ju samma värde som du skrev..?

Kommentaren om största/minsta värde förstår jag inte, men det är (stor!) skillnad mellan att säga att värdemängden är 4 punkter (ditt $V_h$) och att säga att värdemängden är ett helt intervall $[-\frac{34}{5}, -\frac{26}{5}]$. Du testar bara för värden i naturliga talen men x kan vara vilket reellt tal som helst, testa $h(\frac{1}{2}), h(\sqrt{2}),...$, då får du värden som också är i din värdemängd (men du måste beskriva dessa med ett intervall för att det finns oändligt många).

Inabsurdum skrev:

Kommentaren om största/minsta värde förstår jag inte, men det är (stor!) skillnad mellan att säga att värdemängden är 4 punkter (ditt $V_h$) och att säga att värdemängden är ett helt intervall $[-\frac{34}{5}, -\frac{26}{5}]$. Du testar bara för värden i naturliga talen men x kan vara vilket reellt tal som helst, testa $h(\frac{1}{2}), h(\sqrt{2}),...$, då får du värden som också är i din värdemängd (men du måste beskriva dessa med ett intervall för att det finns oändligt många).

Ja juste, du påpekade det till mig tidigare , x kan ju vara vilket reellt tal som helst, eftersom min definitionsmängd är $\mathrm{ℝ}$. Som jag nu testade med massa andra reella tal för x som inte va endast naturliga heltal och dina exempel så är det ju omöjligt att sätta exakt värde för värdemängd? Det blir ju oändligt många som du igen nämnde.

Kort sagt: jag kan inte sätta ett exakt värdemängd, men jag kan däremot sätta intervallet för den alltså $[-\frac{34}{5}, -\frac{26}{5}]$ ?

(Jag tackar så mycket för din tålamod :) )

Ja, fast intervallet blir en exakt beskrivning av värdemängden, om du säger att värdemängden är $[a,b]$ så betyder det alla reella tal mellan a och b (inklusive a och b) vilket är precis vad du vill :-)

Inabsurdum skrev:

Ja, fast intervallet blir en exakt beskrivning av värdemängden, om du säger att värdemängden är $[a,b]$ så betyder det alla reella tal mellan a och b (inklusive a och b) vilket är precis vad du vill :-)

Yess då är jag med denna gång, tusentusen tack :D!