Delbarhet 4

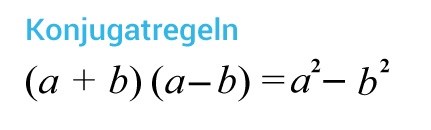 Hej! Jag har fastnat på denna uppgift i ett tag, jag har inte löst sådan matte på ett långt tag så jag är riktigt rostig i hjärnan. Kan någon snälla hjälpa mig komma igång. Jag har en bild av hur jag ska göra då jag vet att jag ska använda konjugatregeln men jag är lite förvirrad då B uttrycket innehåller bara a+b medan i konjugatregeln ingår a-b också. Jag vet inte hur jag ska börja.
Hej! Jag har fastnat på denna uppgift i ett tag, jag har inte löst sådan matte på ett långt tag så jag är riktigt rostig i hjärnan. Kan någon snälla hjälpa mig komma igång. Jag har en bild av hur jag ska göra då jag vet att jag ska använda konjugatregeln men jag är lite förvirrad då B uttrycket innehåller bara a+b medan i konjugatregeln ingår a-b också. Jag vet inte hur jag ska börja.
Tack!
Hej!
Testa att använda konjugatregeln upprepade gånger. Först har du att
Men nu ser du att du kan använda konjugatregeln igen på faktorn . Fortsätt så och se vad du får.
Därefter drar du slutsatsen att är delbar med för att...
Moffen skrev:Hej!
Testa att använda konjugatregeln upprepade gånger. Först har du att
Men nu ser du att du kan använda konjugatregeln igen på faktorn . Fortsätt så och se vad du får.
Därefter drar du slutsatsen att är delbar med för att...
Ah ja jag förstår.
Då kommer man fram till att B är massa faktorer till A och därmed är A delbart med B tänker jag.
Tack för ditt svar!
Det är alltid delbart eftersom man dividerar bort B alltid, som finns i A. Hur det skulle bevisa vet jag dock inte, tyvärr. Hoppas någon annan kan svara. (Mitt tips är att alltid skriva upp allt noga, mer än noga, så ser du lättare)
Om om b är alla positiva faktorer, då kan vi säga att alla de negativa faktorer (de som har ett minus imellan istället för plus) kallas för c så att och då ville vi alltså visa att har en faktor b i sig, vilket den har så att vilket är faktorerna med ett minustecken imellan.
Lite slarvigt uttryckt men jag hoppas det är förståeligt.


