Delbarhet med 3
Hej,
Jag försöker förstå följande matematiska resonemang.
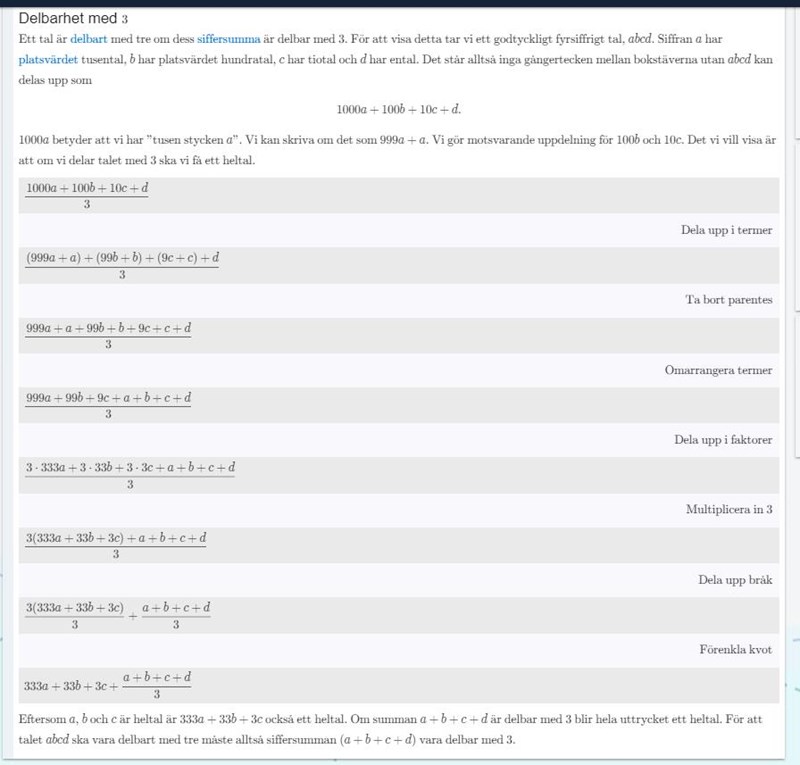
Jag förstår allt förutom sista textstycket.

Tacksam om någon kunde förklara detta på ett annat sätt?
Om talet skall vara delbart med tre skall kvoten
gå jämnt upp och bli ett heltal. När vi delar upp talet ser vi att vi får:
är redan ett heltal, alltså krävs bara att går jämnt upp för att hela talet ska vara delbart med tre. Om går jämnt upp betyder det att är delbart med tre, alltså krävs att siffersumman () är delbar med tre för att hela talet ska vara delbart med tre.
Säger du att du förstår allt ("till och med")? Vad är det du inte förstår?
Vad är det du inte förstår?
Eftersom , och är heltal är också ett heltal.
Är detta otydligt?
Om summan är delbart med tre är hela uttrycket ett heltal.
Är detta obegripligt?
För att talet ska vara delbart med tre måste siffersumman vara delbar med 3.
Är det detta som är konstigt?




