Den här geometriska summan kan väl inte vara rätt?
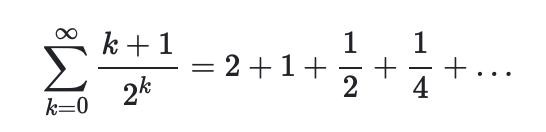 Hur kan första termen vara 2, när den bör vara:
Hur kan första termen vara 2, när den bör vara:
Mer än början som inte stämmer. Vänstersidan är ingen geometrisk summa öht.
Var har du hittat uppgiften och hur lyder den?
Ladda gärna upp en bild.
Notera att det bara är en likhet, vi påstår inte att de två summorna är termvis lika utan att summan på vänstra sidan motsvarar samma reella tal som den på högre sidan (på samma sätt som att 1+3=2+2 utan att 1 är lika med 2). Genom att dela upp den ursprungliga summan i olika delar (och ändra summationsordning) så kan man se att VL=HL.
Alternativ lösningsmetodik:
Mulitplicera med
Derivera med avseende på :
Sätt :
...
Hej D. F.,
För ett ändligt är partialsumman detta tal.
Splittra upp de enskilda termerna.
Addera längs kolumnerna.
Jag fattar inte hur de kan få 2 som första term när det är helt orimligt
Dualitetsförhållandet skrev:Jag fattar inte hur de kan få 2 som första term när det är helt orimligt
Det är inte samma serie. Det är 2 helt olika serier som råkar ha samma svar om du räknar ihop hela.
Va? Förstår ingenting
Bilden du (TS) laddade upp är ett bevis. Det visar när två helt olika serier är lika med varandra. När serien i vänsterled summeras till oändligheten då är summan lika med när serien i högerled summeras till oändligheten. Lägg märke till användandet av oändligheten. Det antyder att serierna inte är termvis lika, som du påpekade i början.
Jämför följande utsaga:
4 + 7 + 3 = 1 + 5 + 8
Likheten gäller trots att summan i VL och HL innehåller helt olika termer.





