Denna omskrivning komplex tal

Förstår ej varför cos-11pi /6 inte blir ett negativt tal när vid omskrivningen? Är det för att det är alltid blir positiva vid omskrivning av tal i första och fjärde kvadranten (kvadranterna på höger sida)?

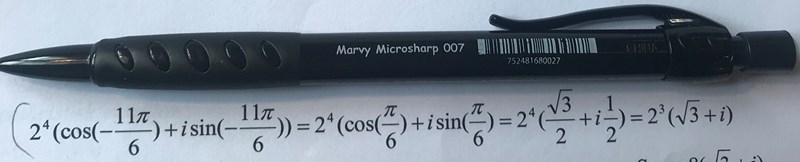
jag får ett negativt tal eftersom att det står minus i täljaren men det spelar alltså ingen roll? Hur ska man veta när det spelar roll eller inte?

Rita in -11pi/6 i enhetscirkeln. Vilken kvadrant ligger den vinkeln i?

Ture skrev:
Rita in -11pi/6 i enhetscirkeln. Vilken kvadrant ligger den vinkeln i?

Första?

Maremare skrev:
Ture skrev:
Rita in -11pi/6 i enhetscirkeln. Vilken kvadrant ligger den vinkeln i?
Första?

Just det, -11pi/6 är samma sak som pi/6, därför är cos(-11pi/6) positv

Ture skrev:
Maremare skrev:
Ture skrev:
Rita in -11pi/6 i enhetscirkeln. Vilken kvadrant ligger den vinkeln i?
Första?
Just det, -11pi/6 är samma sak som pi/6, därför är cos(-11pi/6) positv

ja men när jag tittar i min formelsamling så står det för 11pi / 6 för cos så är det roten ur 3 / 2 och då tänker jag att om jag sätter ett minus framför det så bordet det ju bli minus roten ur 3 / 2 ?

förstår inte varför minustecknet försvinner?

En trigonometrisk identitet säger att $\cos (- v) = \cos v$ det vill säga att $\cos (\frac{11 π}{6}) = \cos (330 °) = \cos (- 30 °) = \cos (- \frac{π}{6}) = \cos (\frac{π}{6})$ . För att bevisa identiteten räcker det med att kolla på enhetscirkeln.

Maremare skrev:

ja men när jag tittar i min formelsamling så står det för 11pi / 6 för cos så är det roten ur 3 / 2 och då tänker jag att om jag sätter ett minus framför det så bordet det ju bli minus roten ur 3 / 2 ?
förstår inte varför minustecknet försvinner?

Det samband du försöker använda är f(-x) = -f(x).

Det sambandet gäller för en viss typ av funktioner som kallas udda funktioner.

Exempel på sådana funktioner är f(x) = sin(x), f(x) = tan(x), f(x) = x, f(x) = x^3 och så vidare.

Det finns även något som heter jämna funktioner. För dessa gäller istället sambandet f(-x) = f(x).

Exempel på jämna funktioner är f(x) = cos(x), f(x) = konstant, f(x) = x^2 och så vidare.

Och så finns det funktioner som varken är jämna eller udda, exempel f(x) = a^x, f(x) = x^2 + 4x och så vidare.

-----------

Eftersom cosinus är en jämn funktion så gäller det alltså inte att cos(-11pi/6) = -cos(11pi/6).

Istället gäller att cos(-11pi/6) = cos(11pi/6).

Okej så alla cos (-v) = cos (v) ?

Maremare skrev:
Okej så alla cos (-v) = cos (v) ?

Ja och det kan du se med hjälp av enhetscirkeln eller med hjälp av grafen till y = cos(x).

På samma sätt kan du se att sin(-v) = -sin(v) flr alla v.

Yngve skrev:
Maremare skrev:
Okej så alla cos (-v) = cos (v) ?
Ja och det kan du se med hjälp av enhetscirkeln eller med hjälp av grafen till y = cos(x).
På samma sätt kan du se att sin(-v) = -sin(v) flr alla v.

Tack!

Svara

Visa senaste svar