Derivata
Hej när jag ska lösa den här frågan tänker jag att jag :
H´(2) = f´(2)-g´(2)
f prim 2 = -1,5
Men när jag ska lösa g prim 2, varför kan jag ej använda mig av derivatans definition och använda mig av punkterna (2:3) och (2,2;3,2) ---> -0,1
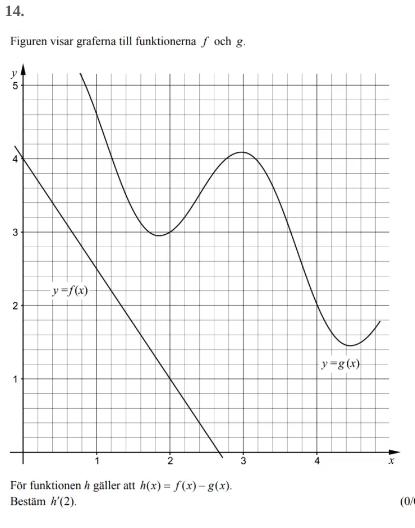
Hej.
Du har rött i att h'(2) = f'(2)-g'(2) och att du ska försöka läsa ut f'(2) och g'(2) ur bilden.
Det stämmer även att f'(2) = -1,5.
Men hur får du att g'(2) är negativ?
Lutningen på grafen till y = g(x) är ju positiv vid x = 2.
(Och ett bättre sätt att uppskatta g'(2) är att rita en tangent till y = g(x) vid x = 2 och beräkna dess lutning.)
Yngve skrev:Hej.
Du har rött i att h'(2) = f'(2)-g'(2) och att du ska försöka läsa ut f'(2) och g'(2) ur bilden.
Det stämmer även att f'(2) = -1,5.
Men hur får du att g'(2) är negativ?
Lutningen på grafen till y = g(x) är ju positiv vid x = 2.
jag skrev fel jag menar 0,1 men varför får jag fel svar?
- Rita en tangent vid x = 2.
- Rita en linje (sekant) genom de två punkter du har valt.
Du kommer att se att dessa linjer har olika lutning.
Din uppskattning av derivatan var alltför grov.
Yngve skrev:
- Rita en tangent vid x = 2.
- Rita en linje (sekant) genom de två punkter du har valt.
Du kommer att se att dessa linjer har olika lutning.
Din uppskattning av derivatan var alltför grov.
men en fråga påverkar avståndet mellan punkterna derivantan, när man använder derivatans definition, och är det bättre att använda längre avstånd eller kortare?
och en till fråga när använder man då derivatans definition?
Ja, det påverkar.
Om du ska approximera en tangent med en sekant så gäller att ju mindre avstånd mellan punkterna desto bättre approximation.
Om du låter avståndet gå mot 0 så kommer sekanten att sammanfalla med tangenten.
Det är precis det som är derivatans definition
=============
Men problemet med att försöka avläsa derivatans värde med hjälp av en sekant är att
- det är väldigt svårt att avläsa koordinaterna för två punkter som ligger nära varandra
- det blir väldigt godtyckligt om vi väljer två punkter som ligger långt ifrån varandra
Därför är det bättre att försöka rita en tangent vid den aktuella punkten och sedan välja två punkter långt ifrån varandra på den tangenten.
Yngve skrev:Ja, det påverkar.
Om du ska approximera en tangent med en sekant så gäller att ju mindre avstånd mellan punkterna desto bättre approximation.
Om du låter avståndet gå mot 0 så kommer sekanten att sammanfalla med tangenten.
Det är precis det som är derivatans definition
=============
Men problemet med att avläsa derivatans värde med hjälp av en sekant är att
- det är väldigt svårt att avläsa koordinaterna för två punkter som ligger nära varandra
- det blir väldigt godtyckligt om vi väljer två punkter som ligger långt ifrån varandra
Därför är det bättre att försöka rita en tangent vid den aktuella punkten och sedan välja två punkter långt ifrån varandra på den tangenten.
När man använder sig av derivatans definition är det då att man har ritat en sekant?
I praktiken använder man aldrig derivatans definition när man ska uppskatta ett derivatavärde ur en graf.
Kategorisering - Tråden flyttad från Alla trådar till Derivata. /admin



