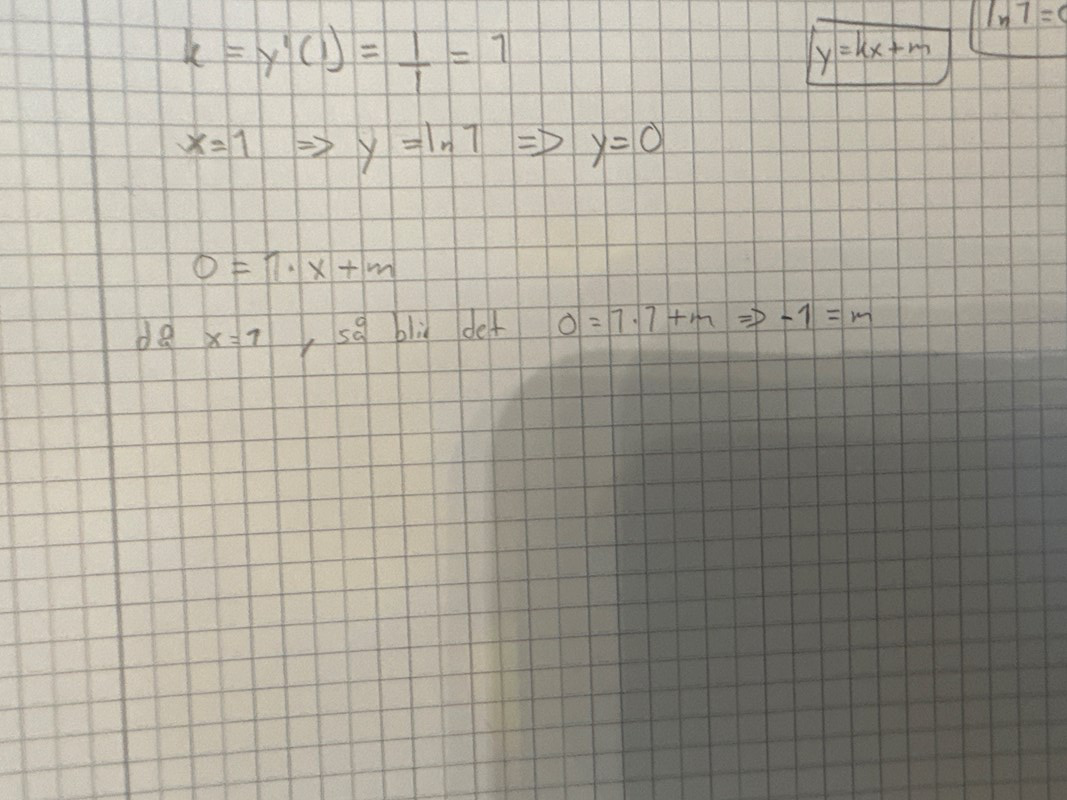Derivata

Det är en bra början. Derivera och räkna ut y'(1) så har du k för punkten y(1).

y'=1/x så där x=1 är k=y'(1)=1. Så långt allt rätt!

Sedan har du räta linjens ekvation: y=kx+m

Du har ett värde på k och kan alltså skriva: y=1x+m

Nu behöver du bestämma m. Då behöver du en punkt (x,y) på den räta linjen också.

Det stämmer, men det inringade är jag lite tveksam till.

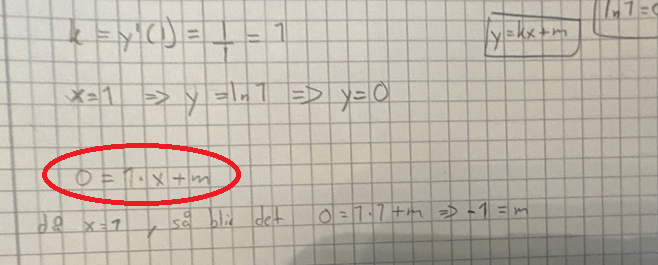
Där borde det stå y=1x+m.

Sedan sätter du in (1,0) i ekvationen och får 0=1*1+m, vilket ger m=-1.

Sen är jag fundersamt hur jag ska fortsätta för att rita kurvan. sätter man bara in x-värden i y=lnx?

noll går ej isåfall 

Biorr skrev:

Sen är jag fundersamt hur jag ska fortsätta för att rita kurvan. sätter man bara in x-värden i y=lnx?

noll går ej isåfall 

Japp! Bara att sätta in x-värden (för x>0) och rita in tillräckligt många (x,y) för att du skall se hur den ser ut.

sictransit skrev:

Biorr skrev:

Sen är jag fundersamt hur jag ska fortsätta för att rita kurvan. sätter man bara in x-värden i y=lnx?

noll går ej isåfall 

Japp! Bara att sätta in x-värden (för x>0) och rita in tillräckligt många (x,y) för att du skall se hur den ser ut.

När du ritar så var särskilt noga med vad som händer när x närmar sig 0. Testa x=0,1 x=0,01, x=0,001 så ser du vad som händer.

Saken är nu så att man inte får använda miniräknare i uppgiften

här var en liknande uppgift

Ja, då vet du i alla fall hur funktionen f(x)=ln(x) ser ut. 

Du vet också att f(1)=0 och att f(e)=1, så där har du två punkter.

Sedan sticker den ned mot -∞ när x närmar sig 0.

Borde vara bra nog för en skiss?

hur man beräknar tangentens ekvation förstår jag, men inte hur man ska rita ut kurvan (tillvägagångssättet)

vart kommer e ifrån?

Biorr skrev:

hur man beräknar tangentens ekvation förstår jag, men inte hur man ska rita ut kurvan (tillvägagångssättet)

vart kommer e ifrån?

Talet e är basen för de naturliga logaritmerna, på samma sätt 10 är basen för 10-logaritmerna.

log(10)=1 eftersom 10^1=10
ln(e)=1 eftersom e^1=e

e är ungefär 2,718

Tillvägagångssättet är att du stoppar in olika värden på x i funktionen f(x)=ln(x). Ut trillar då y-värden. Dessa punkter (x,y) markerar du i ett diagram.

Eftersom du inte får använda miniräknare, så är det ju lite klurigt att beräkna ln(x). Dock är ju f(1) och f(e) lätta.

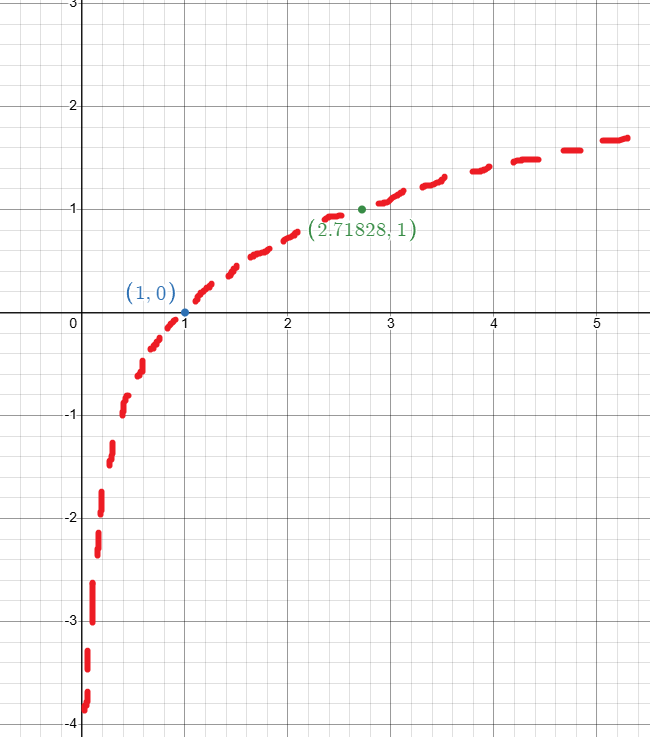
Ju fler punkter du har desto bättre uppfattning om kurvans utseende får du. 

I det här fallet har jag bara två och dessutom vet jag att kurvan skall sticka iväg mot -∞. Det får duga.

Annars får man försöka räkna fram en till. Om du får använda papper och penna, så kan du ju räkna ut vad e^2 är. Då har du en punkt till att rita in (e^2, 2). 

Rita tangenten kräver bara en linjal. :-)