Derivata kedjeregeln absolutbelopp
Hej, jag ska ta derivatan av ln(abs(ln(abs(x)))).
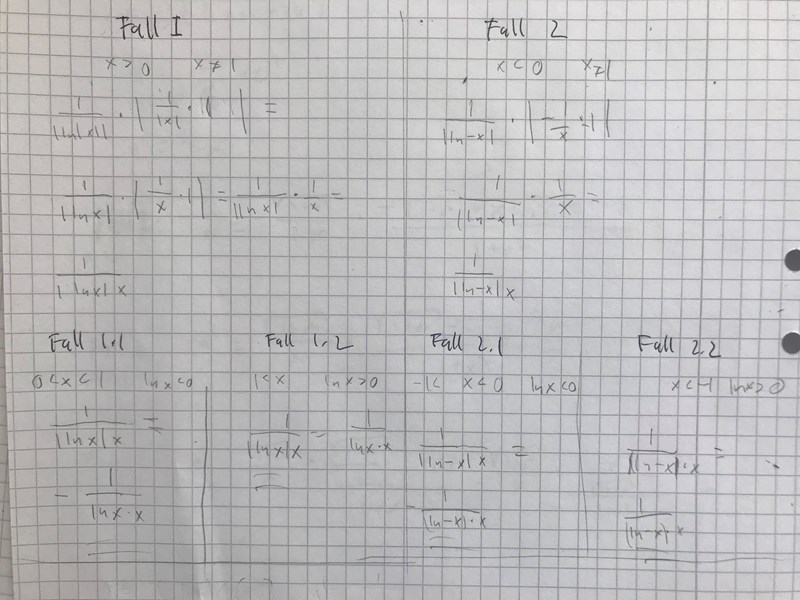
Då får jag fyra olika fall (brukar av vana dela upp i fall när jag använder absolutbelopp) men enligt facit och wolfram stämmer bara ett av dem. Vad är det som är fel och varför ska man inte dela upp i fall nu?
Edit: (står lite fel under fall 2.1/2.2 ska vara ln -x </>0)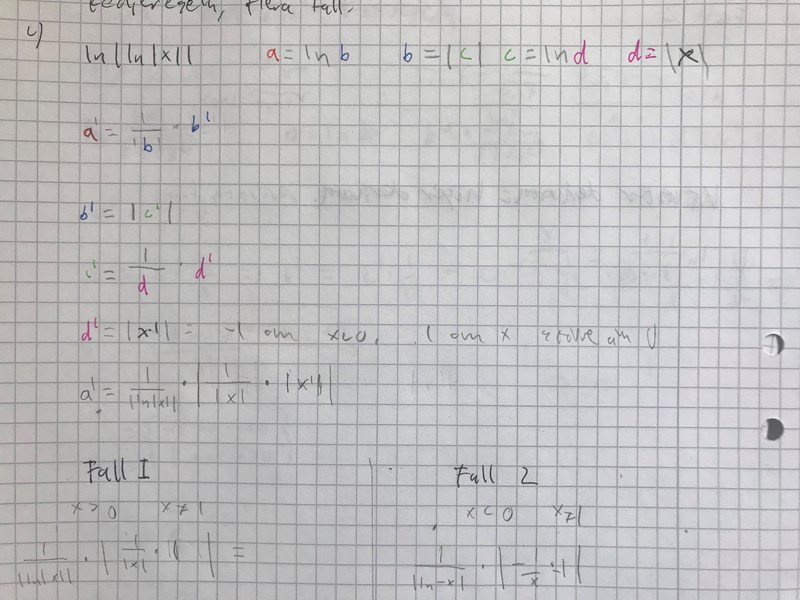
kan som bekant delas upp i två fall, . Är definierat för båda dessa fall? :)
ln a är definierad för alla reella a >= 0.
|x| >= 0 är definierad för alla x
detta medför att ln|x| är definierad för alla x tänker jag.
Om x är negativt blir ln|x|=ln-x vilket är definierat. (om x är negativt medför att -x är positivt)
Skriv om det annars som:
Nästan rätt. Är ln(0) definierat?
Hej,
Logaritmen är inte definierad i noll och logaritmen av 1 är lika med noll, vilket gör att din funktion är odefinierad på mängden
- Fall 1. Här är och
- Fall 2. Här är och
- Fall 3. Här är och
- Fall 4. Här är och
Men det stämmer alltså att det korrekta är att dela upp det i fall och att facit slarvade lite?
ugglebulle skrev:Men det stämmer alltså att det korrekta är att dela upp det i fall och att facit slarvade lite?
Enligt mig, ja.
Bra, tack så mycket!



