Derivata, kedjeregeln - Rektangel i koordinatsystem (origo 4, upg. 3147)

Hej,

Har fastnat på denna uppgift:
Detta är min lösning, men den är inte fullständig.

Undrar hur jag ska göra nu, för att hitta största arean tar man ju A'(x) = 0 och sedan kontrollerar maximivärdet med andraderivatan och till sist sätter jag in maximivärdet i funktionen, men hur ska jag ta andraderivatan av en sammansatt funktion (har inte gått igenom andra deriveringsregler för mer komplexa funktioner än)? Har jag ens gjort rätt eller finns det en smidigare metod?

Tack på förhand!

D( f(x)*g(x) ) = f'(x)*g(x) + f(x)*g'(x)

Hur fick du fram detta samband? Bygger det på kedjeregeln?

Sambandet som Bubo skrivit kallas för produktregeln. Det är en av räknelagarna som man lär sig i Matematik 4.

Ifall ni ännu inte gått igenom produktregeln, så kan man faktiskt klara sig med enbart kedjeregeln:

Tänk dig att $A(x) = 2x \, \sqrt{3-x^2} = \sqrt{4x^2}\, \sqrt{3-x^2} = \sqrt{12x^2 - 4x^4}$ . Du kan alltså bestämma $A^\prime(x)$ m.h.a. kedjeregeln, där rotdragning är yttre funktionen och polynomet $12x^2 - 4x^4$ utgör inre funktionen.

En smidigare lösning efterfrågas (har kanske inte med den aktuella kursen att göra):

Kurvan är egentligen x² + y² =3 d v s en cirkel med radie sqr(3). Då kan ett hörn tecknas

(sqr3)(cos x, sin x) och ytan blir $\sqrt{3} \sin x \cdot 2 \cdot \sqrt{3} \cos x = 3 \cdot 2 \cdot \sin x \cdot \cos x = 3 \sin 2 x$

som har max för x=45 grader i intervallet o<x<90 grader.

LuMa07 skrev:
Sambandet som Bubo skrivit kallas för produktregeln. Det är en av räknelagarna som man lär sig i Matematik 4.

Ifall ni ännu inte gått igenom produktregeln, så kan man faktiskt klara sig med enbart kedjeregeln:

Tänk dig att $A(x) = 2x \, \sqrt{3-x^2} = \sqrt{4x^2}\, \sqrt{3-x^2} = \sqrt{12x^2 - 4x^4}$ . Du kan alltså bestämma $A^\prime(x)$ m.h.a. kedjeregeln, där rotdragning är yttre funktionen och polynomet $12x^2 - 4x^4$ utgör inre funktionen.

Tack LuMa07, detta underlättade verkligen! Kom fram till rätt svar, bifogar min lösning nedan: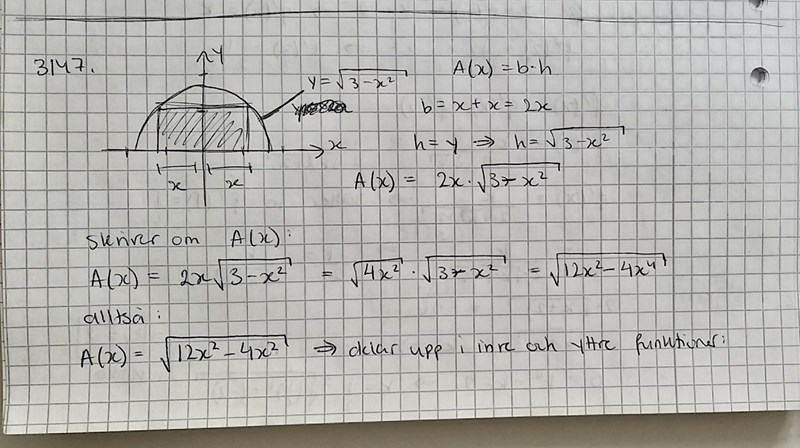

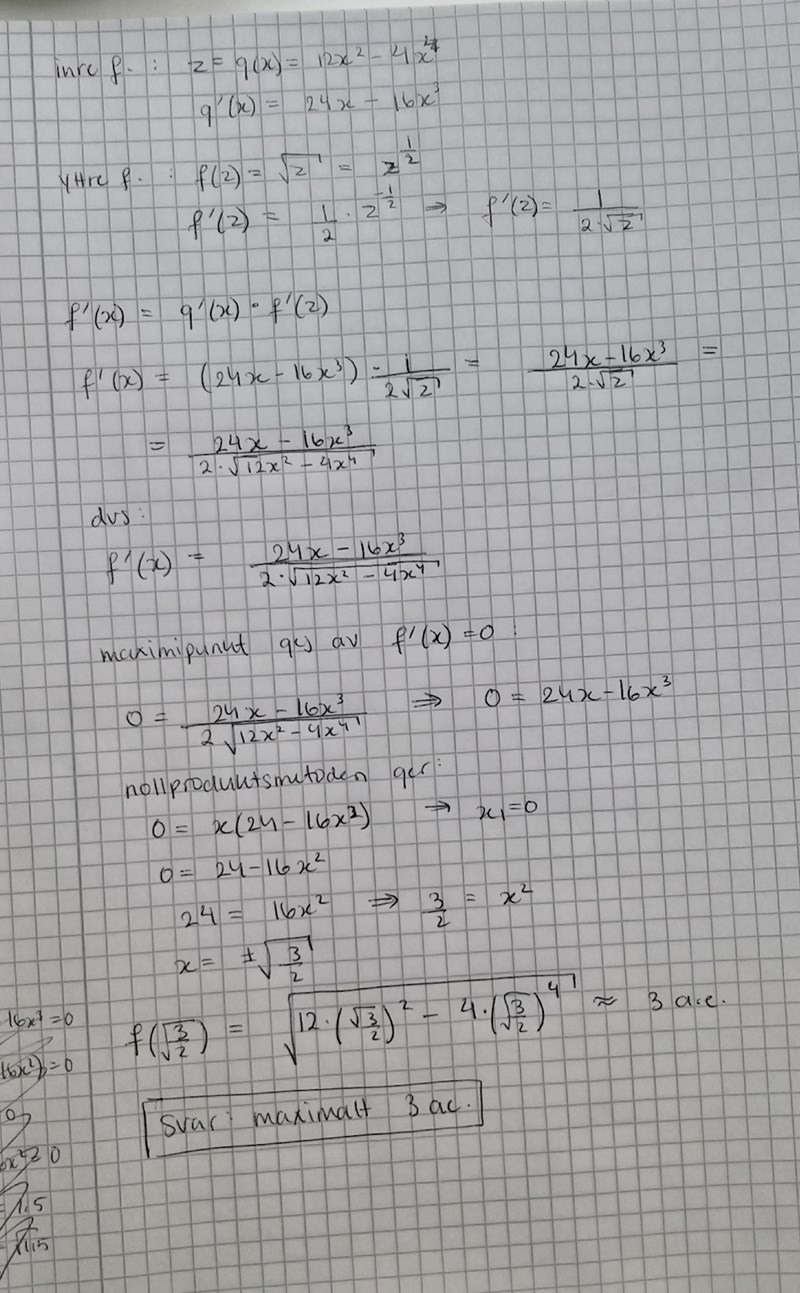
hansa skrev:
En smidigare lösning efterfrågas (har kanske inte med den aktuella kursen att göra):

Kurvan är egentligen x² + y² =3 d v s en cirkel med radie sqr(3). Då kan ett hörn tecknas

(sqr3)(cos x, sin x) och ytan blir $\sqrt{3} \sin x \cdot 2 \cdot \sqrt{3} \cos x = 3 \cdot 2 \cdot \sin x \cdot \cos x = 3 \sin 2 x$

som har max för x=45 grader i intervallet o<x<90 grader.

Är detta cirkelns ekvation? Ingick inte i kurs 3c när jag läste det under höstterminen, men tack för din alternativa lösning, Hansa!

Ett alternativ kommer här. Det börjar rätt lika som ditt, men jag använde sedan både kedje- och produktregeln.

ConnyN skrev:
Ett alternativ kommer här. Det börjar rätt lika som ditt, men jag använde sedan både kedje- och produktregeln.

Hej,
Tack för ditt svar, ConnyN! Jag anade att det hade något med de andra reglerna att göra men vi har ännu inte gått igenom dem än.

Svara

Visa senaste svar