Derivata och asymptoter
Hej, har stött på två olika frågor som jag har problem med att beräkna:
1. När jag studerar olika grafer. T.ex. följande: f(x) = 1x2 f(x) = 12x2 och f(x) = 4x2
Hur kan jag se skillnad på dessa om de ritas upp i ett koordinatsystem. Hur ser man vilken som växer mest/minst? T.ex. i följande uppgift:
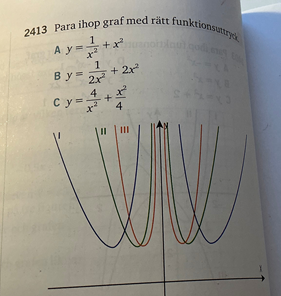
Här kan jag utgå från den funktion som dominerar för stora x: x^2 eller för den som dominerar för små x (polynomdivisionuttrycket). Jag vet att den orange funktionen motsvarar B eftersom den växer fortast för stora X. Den gröna motsvarar A. Den blå måste då motsvara C eftersom den växer långsamt för stora x.
Om jag vill utgå från små värden på x får jag dock ett annat svar. 4/x^2 växer fortare än 1 /2x^2 och då borde C bli orange och B bli blå. Alltså tvärtom. Vad är det jag missar?
2. Derivera: f(x) = 2xlnx och f(x) = 3xx.
Varför kan man inte göra på följande sätt i den första: f'(x) = f'(x) =2*lnx*xlnx-1* (1/x) = f'(x) = 2lnxx* x^lnx - 1
Dvs. betrakta lnx som en inre derivata och 2x^n som en yttre derivata?
Definiera g(x) = 1/x2 + x2.
Då gäller
A) y = g(x)
B) y = g(√2x)
C) y = g(12x)
Säg att g(x) har ett minvärde då x = a. g(kx) får då ett motsvarande minvärde då kx = a, dvs då x = a/k. Hoppas att detta ger en ledning till hur man kan tänka.
På 2. skriv x som elnx. Då kan du sedan använda kedjeregeln.
Precis. Det var det jag undra. Måste man alltid skriva om till basen e? Kan man inte betrakta funktionen som x^n och sedan derivera? Därefter multiplicera med n' om n är den inre funktionen?
Vilken är din inre funktion? Vilken är din yttre funktion?
Inre funktion y(x) = lnx?
Yttre funktion z(y) = yn?
h(x) = z(y(x)) = z(lnx) = (lnx)n.
Det blir inte rätt som du ser.
Så man måste alltid göra om till basen e?
Du kan även använda så kallad logaritmisk derivering.
f'(x)f(x)=(ln(f(x)))'.
