derivata samt för vilka x derivatan existerar (envariabelanalys)

jag ska derivera $f (x) = \ln (| \sin x |)$ och avgöra för vilka x derivatan existerar

lösning:

d/dx ln x = 1 /x

d/dx |x| = x/|x|

d/dx = sinx = cosx

detta ger mig:

$f' (x) = \frac{1}{|\sin x|} d / d x |\sin x| = \frac{1}{|\sin x|} \frac{\sin x}{| \sin x |} d / d x \sin x = \frac{1}{|\sin x|} \frac{\sin x}{|\sin x|} \cos x = \frac{1}{| \sin x |} \frac{\sin x \cos x}{|\sin x|} = \frac{\sin x \cos x}{{(|\sin x|)}^{2}}$

stämmer den derivatan om man inte får använda cotx? ser lite grötigt ut, eller är det tänkt att man ska skriva om det på något sätt?

Gällande för vilka x derivatan existerar så räknar för vilka x vi inte får sinx = 0

och det ger mig $x \neq π + 2 πn och x \neq 2 πn$ där n tillhör något reellt tal

är det så man kan göra eller är det något som är fel eller saknas?

$\frac{\sin x}{{|\sin x|}^{2}} = \frac{1}{\sin x} .$

PATENTERAMERA skrev:
$\frac{\sin x}{{|\sin x|}^{2}} = \frac{1}{\sin x} .$

okej så jag kan förenkla sådär utan att förklara något mer (tänker att det är abs belopp i nämnaren)

gällande derivatans existens då?

${|a|}^{2} = a^{2}, \forall a \in ℝ$ . Således har vi att $\frac{\sin x}{{|\sin x|}^{2}} = \frac{\sin x}{\sin^{2} x} = \frac{1}{\sin x} .$

PATENTERAMERA skrev:
${|a|}^{2} = a^{2}, \forall a \in ℝ$ . Således har vi att $\frac{\sin x}{{|\sin x|}^{2}} = \frac{\sin x}{\sin^{2} x} = \frac{1}{\sin x} .$

okej tack då är jag med

gällande derivatans existens då?

Om vi definierar g(x) = ln $|x|$ , så är g(x) definierad för alla reella tal x - utom för x = 0. g är dessutom deriverbar överallt där den är definierad och g'(x) = 1/x.

Vi har då att f är sammansättningen mellan g och sinusfunktionen.

f(x) = (g $\circ$ sin)(x), f(x) är definerad överallt, utom då sin(x) = 0, dvs x = n $π$ .

Om vi nu antar x har ett värde där f(x) är definierad så kan vi beräkna dervitan med hjälp av kedjeregeln.

f'(x) = g'(sin(x)) $\cdot$ sin'(x) = $\frac{1}{\sin x} \cdot \cos x = c o t x$ .

PATENTERAMERA skrev:
Om vi definierar g(x) = ln $|x|$ , så är g(x) definierad för alla reella tal x - utom för x = 0. g är dessutom deriverbar överallt där den är definierad och g'(x) = 1/x.
Vi har då att f är sammansättningen mellan g och sinusfunktionen.
f(x) = (g $\circ$ sin)(x), f(x) är definerad överallt, utom då sin(x) = 0, dvs x = n $π$ .
Om vi nu antar x har ett värde där f(x) är definierad så kan vi beräkna dervitan med hjälp av kedjeregeln.
f'(x) = g'(sin(x)) $\cdot$ sin'(x) = $\frac{1}{\sin x} \cdot \cos x = c o t x$ .

okej men stämmer min utsaga

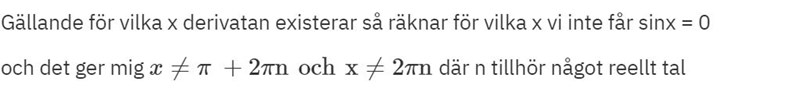
så derivatan existerar för alla x skilt från pi + 2pin och x skilt från 2pi n där n är ett godtyckligt tal?

Ja. Men det är kanske snyggare att skriva x $\neq$ n $π$ , som täcker in båda alternativen på ett mera kompakt sätt.

Om man skriver f’(x) = cotx, så borde man kanske inte behöva säga något mer, eftersom x = n $π$ inte ingår i definitionsmängden till cotx, så det är så att säga implicit vilka x som är undantagna, tycker jag.

Varför säger du att du inte får använda cotx?

PATENTERAMERA skrev:
Ja. Men det är kanske snyggare att skriva x $\neq$ n $π$ , som täcker in båda alternativen på ett mera kompakt sätt.
Om man skriver f’(x) = cotx, så borde man kanske inte behöva säga något mer, eftersom x = n $π$ inte ingår i definitionsmängden till cotx, så det är så att säga implicit vilka x som är undantagna, tycker jag.
Varför säger du att du inte får använda cotx?

aa okej okej tack för hjälpen!

eller får och får, de har meddelat att de inte kommer ha tal/eller gå igenom cotx i kursen så jag är inte riktigt bekant det cotx

Svara Avbryt

Visa senaste svar