derivata / tangentens ekvation
hej,
tyckte denna uppgiften var lite lurig:
 Jag har deriverat y=ln2x till y'=1/x och satt då in detta som k i y=kx+m (m som då inte finns för den går genom origo)
Jag har deriverat y=ln2x till y'=1/x och satt då in detta som k i y=kx+m (m som då inte finns för den går genom origo)
om jag sätter in det blir det inte rätt, så jag tänkte utifrån tangeringspunkten som blir (x , ln2x) och använde mig av k = (y2-y1)/(x2-x1) och fick fram (ln2x-0)/(x-0) så ln(2x)/x = 1/x (fattar inte riktigt varför jag gjorde det, desperat försök) och fick ln2x = 1 , utifrån detta får jag x = e/2 och om jag sätter in det i y=(1/x)*x +m får jag ju y=(2/e)x som är rätt,
men jag förstår inte varför jag inte får rätt om jag bara sätter in k som 1/x och varför jag behöver få ut x genom k=y2-y1/x2-x1
^ om jag inte är helt ute och cyklar, hade uppskattat förklaring till varför man ska göra så eller om det finns ett bättre sätt, tack!
Hej.
Kontrollera din derivering.
Yngve skrev:Hej.
Kontrollera din derivering.
y=ln2x y'=1/2x * 2 = 1/x ? eller?
y(x)=ln(2x)
y'(x)=1/x
I punkten (a,ln(2a)) är tangentens tangentens ekvation
t(x)=y(a)+y'(a)(x-a)=ln(2a)+1/a(x-a)
t(0)=0 ger a=e/2
varför
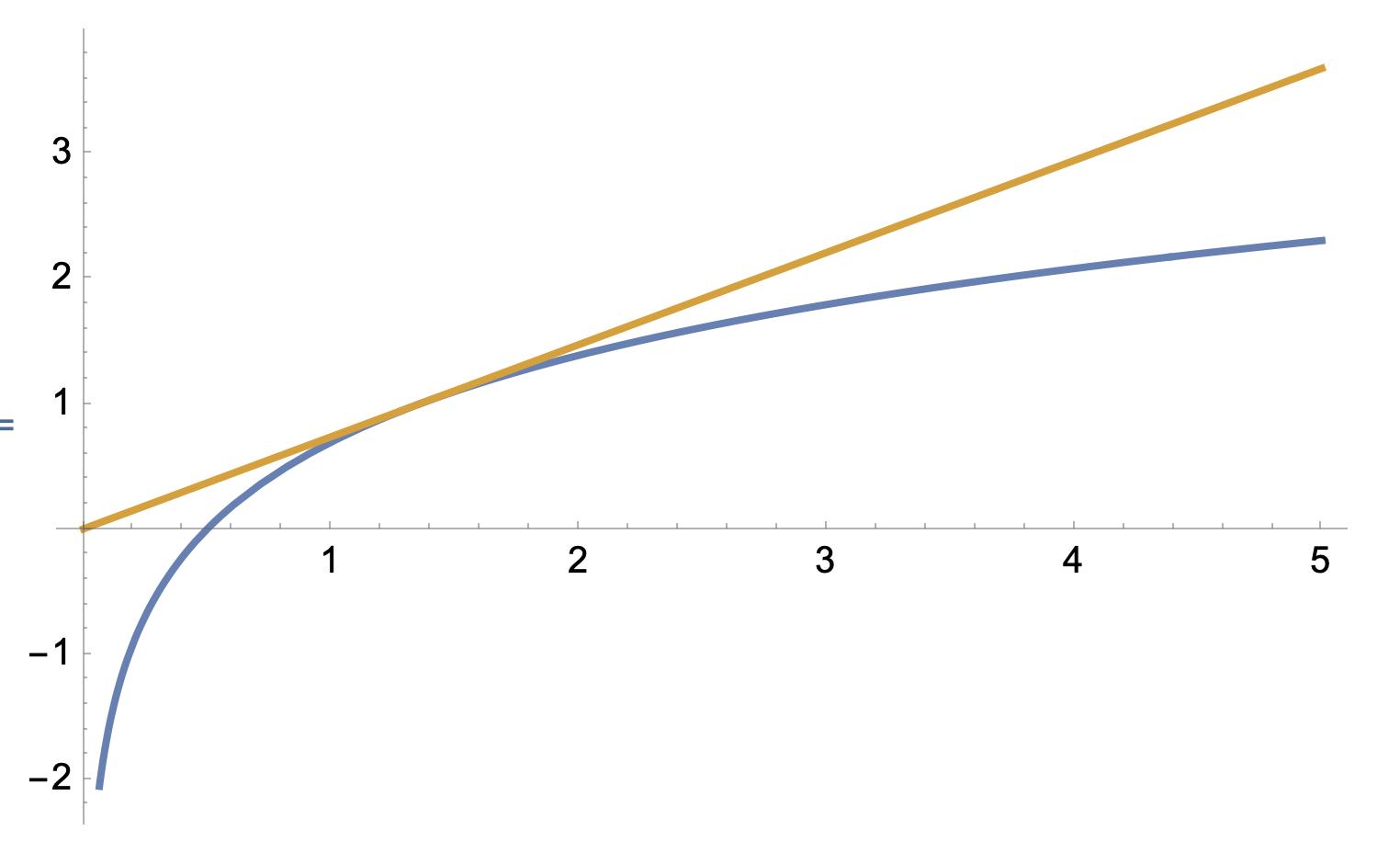
t(x)=ln(2*e/2)+1/(e/2)(x-e/2)=2x/e.
veerleeloise skrev:
y=ln2x y'=1/2x * 2 = 1/x ? eller?
Ja, jag tänkte fel.
tror jag förstår lite mer nu, tack båda!


