Derivatan av cos (x^2)
Hej! Jag löste uppgiften genom att ange F'(x) som -2xsinx2 i första steget. Tydligen är derivatan detsamma som funktionen, dvs cos (x2). Varför? Vilka andra funktioner gäller detta för? Tack på förhand.
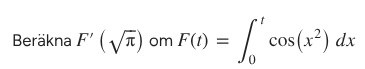
Detta visade sig inte stämma.
Dr.scofield skrev:Hej! Jag löste uppgiften genom att ange F'(x) som -2xsinx2 i första steget. Tydligen är derivatan detsamma som funktionen, dvs cos (x2). Varför? Vilka andra funktioner gäller detta för? Tack på förhand.
Detta visade sig inte stämma.
Är denna fråga aktiv?
Inte den första i och med att jag insåg att påståendet inte stämde. Dessutom var min derivering rätt. Däremot fick jag 0 som slutliga svar på uppgiften? Mitt sista steg såg ut såhär: F'(roten ur pi) = 2*(roten ur pi) * sin(pi) = 0?
Dr.scofield skrev:Inte den första i och med att jag insåg att påståendet inte stämde. Dessutom var min derivering rätt. Däremot fick jag 0 som slutliga svar på uppgiften? Mitt sista steg såg ut såhär: F'(roten ur pi) = 2*(roten ur pi) * sin(pi) = 0?
Säg att vi kan finna en prim.fkn till cos(x^2), vi kallar den C(x). (Den är svår att finna och 'svinig', men vi behöver inte den.)
Då är
F(t) = INT_0^t cos (x^2) = [ C(x) ]_0^t = C(t)-C(0) = C(t)-konstant
Om vi nu deriverar så får vi
F'(t) = C'(t)-0 = cos(t^2)-0 = cos(t^2)
eftersom C(t) var prim.fkn till cos(t^2).
Nu kan du beräkna vad som efterfrågas.
Jag förstår inte riktigt varför du arbetar med "C" och sådant (jag vet inte heller vad det betyder hehe). Jag deriverade helt enkelt funktionen F(x) = cos x2.
Då fick jag F'(x) = -2xsinx2.
Därefter F'(b) - F'(a).
Är det fel?
Dr.scofield skrev:Jag förstår inte riktigt varför du arbetar med "C" och sådant (jag vet inte heller vad det betyder hehe). Jag deriverade helt enkelt funktionen F(x) = cos x2.
Då fick jag F'(x) = -2xsinx2.
Därefter F'(b) - F'(a).
Är det fel?
Ja, det är fel. Hur hade din metod fungerat om
F(t) = INT_0^t 1 dx
?
Jag hade bestämt antiderivatan först. Denna uppgift förvirra mig eftersom de sökte derivatan istället.
Dr.scofield skrev:... Jag deriverade helt enkelt funktionen F(x) = cos x2.
... Är det fel?
Ja, det är fel. Observera att F(x) INTE är lika med cos x2.
I uppgiften står det att F(x) definieras som en integral av cos x2, d.v.s. F(x) är en primitiv till cos x2 (enligt analysens huvudsats). När primitiven deriveras, så får man tillbaka integranden, så F'(x) = cos x2
Det finns inget behov att ta fram antiderivatan (vilket man garanterat kommer att misslyckas med när det gäller just cos x2), eftersom man känner till det teoretiska resultatet att derivatan av en antiderivata ger tillbaka ursprungsfunktionen.
Åhh! Jag förstår vad du menar (även detta med antiderivatan av cos x^2 hehe). Ska försöka lösa uppgiften igen nu.
Skulle jag kunna få första steget till lösningen? Jag vet inte vad jag ska göra med derivatan av funktionen.


