Derivatan till funktionen K(t) med talet e och värde på t när K(t)=0, 000 001

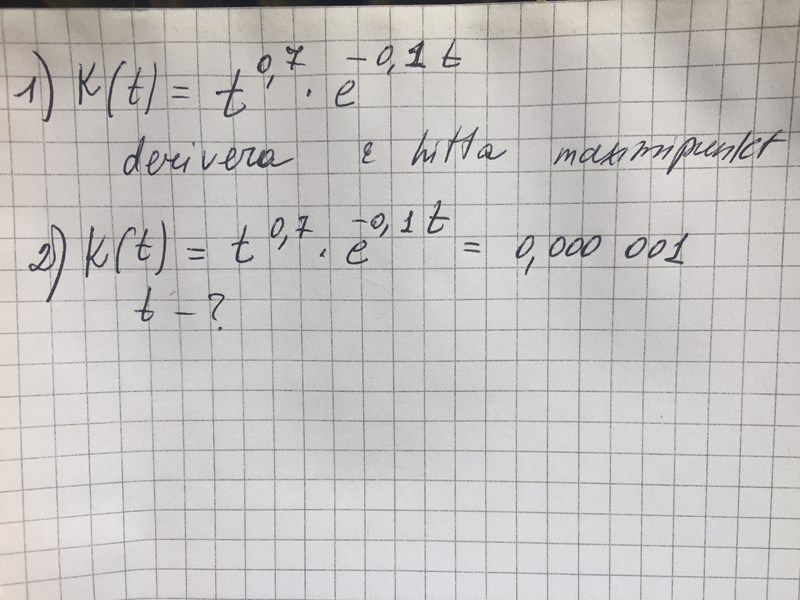
DreamChild skrev :

Hej,

 

Jan kan inte lösa följande uppgifter. Jag är bara intresserad i matematisk lösningen, alltsä själv fråga är super lång, ingen kommer att läsa det, men om ni är intresserad är det en gruppaktivitet i avsnitet 3.3. Deriveringsregler för exponentialfunktioner, matte 3c, boken Exponent 3c.

 

Kan nån hjälpa?

Hej.

1) Använd produktregeln $(fg)'=f'g+fg'$ och använd att derivatan av $e^{kt}$ är $k\cdot e^{kt}$.

Kommer du vidare då?

Det går fel tror jag...

Och det är allt jag kunde göra

Yngve skrev :

DreamChild skrev :

Hej,

 

Jan kan inte lösa följande uppgifter. Jag är bara intresserad i matematisk lösningen, alltsä själv fråga är super lång, ingen kommer att läsa det, men om ni är intresserad är det en gruppaktivitet i avsnitet 3.3. Deriveringsregler för exponentialfunktioner, matte 3c, boken Exponent 3c.

 

Kan nån hjälpa?

Hej.

1) Använd produktregeln $(fg)'=f'g+fg'$ och använd att derivatan av $e^{kt}$ är $k\cdot e^{kt}$.

Kommer du vidare då?

Hej, jag gjorde så, men vet inte vad kan jag göra med det nu

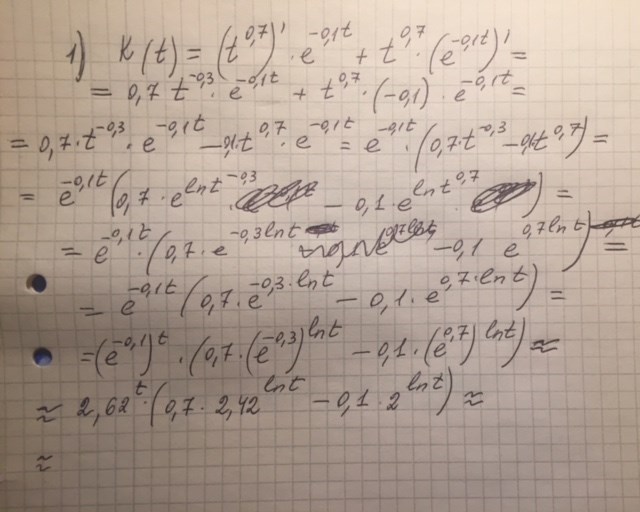
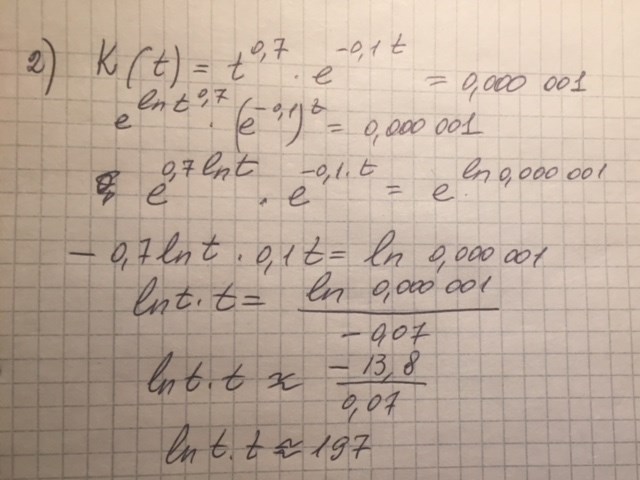
DreamChild skrev :

Yngve skrev :

Visa föregående citat

DreamChild skrev :

Hej,

 

Jan kan inte lösa följande uppgifter. Jag är bara intresserad i matematisk lösningen, alltsä själv fråga är super lång, ingen kommer att läsa det, men om ni är intresserad är det en gruppaktivitet i avsnitet 3.3. Deriveringsregler för exponentialfunktioner, matte 3c, boken Exponent 3c.

 

Kan nån hjälpa?

Hej.

1) Använd produktregeln $(fg)'=f'g+fg'$ och använd att derivatan av $e^{kt}$ är $k\cdot e^{kt}$.

Kommer du vidare då?

Hej, jag gjorde så, men vet inte vad kan jag göra med det nu

 

1) Derivatan är $K'(t)=e^{-0.1t}(0.7t^{-0.3}-0.1t^{0.7})$ och du vill lösa ekvationen $K'(t)=0$ för att hitta ev. extrempunkter.

Eftersom $e^{-0.1t}\neq 0$ så måste det gälla att $0.7t^{-0.3}-0.1t^{0.7}=0$ om ekvationen ska ha någon lösning.

Dividera nu båda led med $0.1$ och $t^{-0.3}$.

Yngve skrev :

DreamChild skrev :

Visa föregående citat

Yngve skrev :

DreamChild skrev :

Hej,

 

Jan kan inte lösa följande uppgifter. Jag är bara intresserad i matematisk lösningen, alltsä själv fråga är super lång, ingen kommer att läsa det, men om ni är intresserad är det en gruppaktivitet i avsnitet 3.3. Deriveringsregler för exponentialfunktioner, matte 3c, boken Exponent 3c.

 

Kan nån hjälpa?

Hej.

1) Använd produktregeln $(fg)'=f'g+fg'$ och använd att derivatan av $e^{kt}$ är $k\cdot e^{kt}$.

Kommer du vidare då?

Hej, jag gjorde så, men vet inte vad kan jag göra med det nu

 

1) Derivatan är $K'(t)=e^{-0.1t}(0.7t^{-0.3}-0.1t^{0.7})$ och du vill lösa ekvationen $K'(t)=0$ för att hitta ev. extrempunkter.

Eftersom $e^{-0.1t}\neq 0$ så måste det gälla att $0.7t^{-0.3}-0.1t^{0.7}=0$ om ekvationen ska ha någon lösning.

Dividera nu båda led med $0.1$ och $t^{-0.3}$.

Tack! Fungerade bra!

Har du några tips för den andra fråga?