Derivator

Frågan är i princip "Hur många unika lösningar har ekvationen $e^{2x}-e^x=a$? Beräkna antalet för varje tal a.". 

Varför använder du dig av asymptoter? Jag förstår inte riktigt motivet till det. Istället för att derivera, genomför substitutionen $t=e^x$ direkt istället, så att du får:

$t^2-t-a=0$

Denna ekvation kan du dra igenom PQ-formeln, så att du får $t=\frac{1}{2}\pm \frac{\sqrt{1+4a}}{2}$. Du kan då substituera tillbaka och få:

$e^x=\frac{1\pm \sqrt{1+4a}}{2}$.

Härifrån kan du läsa av hur många lösningar som finns för varje värde på a. :)

Smutstvätt skrev:

Frågan är i princip "Hur många unika lösningar har ekvationen $e^{2x}-e^x=a$? Beräkna antalet för varje tal a.". 

Varför använder du dig av asymptoter? Jag förstår inte riktigt motivet till det. Istället för att derivera, genomför substitutionen $t=e^x$ direkt istället, så att du får:

$t^2-t-a=0$

Denna ekvation kan du dra igenom PQ-formeln, så att du får $t=\frac{1}{2}\pm \frac{\sqrt{1+4a}}{2}$. Du kan då substituera tillbaka och få:

$e^x=\frac{1\pm \sqrt{1+4a}}{2}$.

Härifrån kan du läsa av hur många lösningar som finns för varje värde på a. :)

Jag gjorde så från början men visste inte hur jag skulle kunna läsa ut antalet lösningar från e^x=(1±sqrt(1+4a)/)2. 

Anledningen till asymptoter är för att kunna rita hur kurvan ser ut och på så sett enklare se och "läsa ut" lösningarna. Förstår inte vad jag gör för fel med m-värdet då x->-inf?!

Hej!

Du har kommit fram till att funktionen $f(x)=(e^{x})^2-e^x-a$ har ett globalt minimum då $x=-\ln 2$. Detta minsta värde är lika med

    $f(-\ln 2) = \frac{1}{4}-\frac{1}{2}-a= -(\frac{1}{4}+a).$

Det betyder att för alla tal $x$ gäller det att $f(x) \geq -(a+0.25).$

Du är intresserad av om det finns något x som är sådant att $f(x) = 0$.

• Om $a=-0.25$ så finns det precis ett sådant $x$, nämligen $x = -\ln 2$.
• Om  $a< -0.25$ så är $f(x) > 0$ för alla $x$.

Detta visar att det intressanta fallet att undersöka är när $a>-0.25$ ...

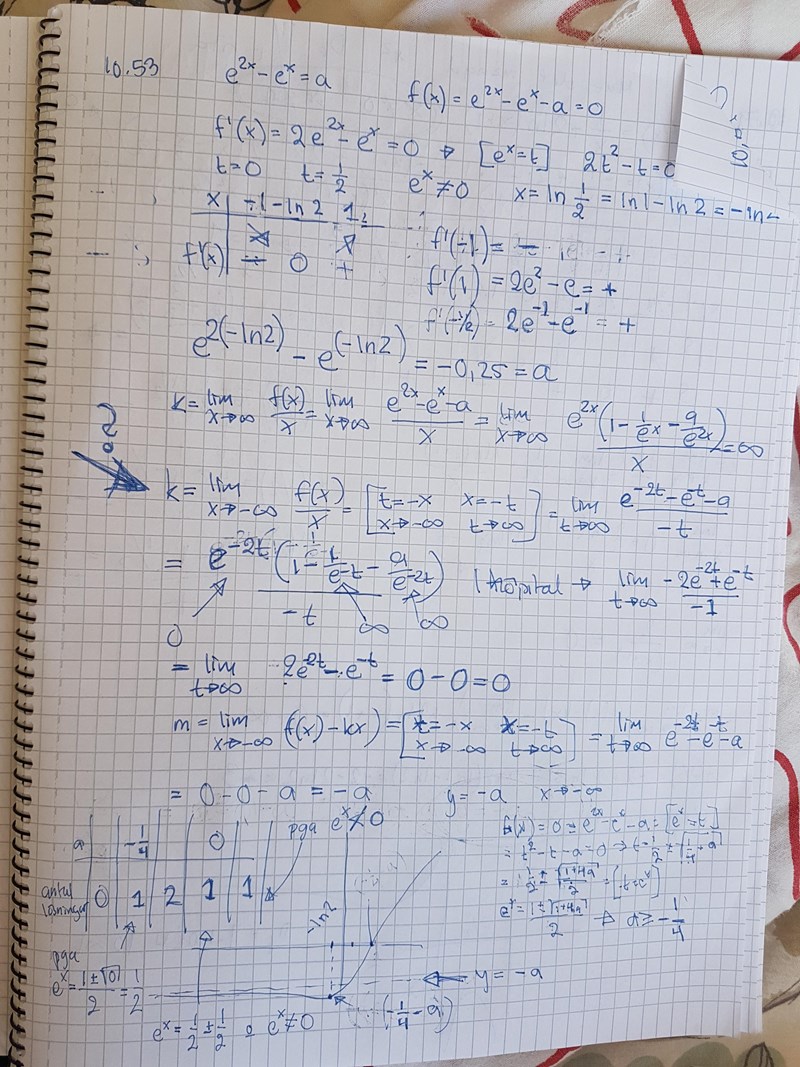Tack för hjälp! Tillsist fattade jag