derivera absolutbelopp (envariabelanalys)
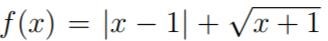
jag ska derivera denna och hitta eventuella nollställe, jag har deriverat och fått detta, men det är bara för att jag har fått för mig att derivatan av absolutbelopp är bara att ställa upp som en kvot som jag har gjort. så med det sagt vet jag inte hur man beräknar ekvationen = 0
om det står 1 eller -1 så kan jag lösa den men har ingen aning vad man gör när den där kvoten existerar med absolutbeloppet.
eller räknar man ut det på något annat sätt?
Dela upp i tre fall verkar enklast (x = 1 är det tredje fallet).
Laguna skrev:Dela upp i tre fall verkar enklast (x = 1 är det tredje fallet).
ska jag dela upp det i 3 fall sen derivera alla 3 eller ska jag derivera och sen dela upp i 3 fall?
Det borde gå på ett ut.
Nja, derivatan av |x-1| är ju odefinierad när x = 1, så det fallet funkar bara innan du deriverar.
Men om du bara ska derivera så behövs inte det fallet. Om du är ute efter att hitta lokala extrempunkter får du däremot ta med det.
Alternativt skriver du istället enligt nedan:
jag ska hitta extrempunkterna men det är inga problem utan min utmaning är hur jag deriverar funktionen samt hittar nollställen till den för jag vet ej hur man räknar när det är en division mellan ett absolutbelopp
Som sagt, dela upp det i olika fall.
Smaragdalena skrev:Som sagt, dela upp det i olika fall.
som sagt, jag har efterfrågat om jag ska göra det innan eller efter jag deriverar
Prova.
Du hade fått fram derivatan i din fråga. Det såg rätt ut.
Men funktionen är inte deriverbar då x = 1 eller -1, och dessutom inte definierad alls för x < -1.
är lika med 1 då x > 1 och lika med -1 då x < 1.
Så om vi betraktar för vilka x > 1 som derivatan blir noll så har vi
1 + = 0, som inte har någon lösning.
Om vi betraktar för vilka x som derivatan blir noll så har vi
-1 + = 0.
Hoppas att detta hjälper dig vidare.
PATENTERAMERA skrev:Du hade fått fram derivatan i din fråga. Det såg rätt ut.
Men funktionen är inte deriverbar då x = 1 eller -1, och dessutom inte definierad alls för x < -1.
är lika med 1 då x > 1 och lika med -1 då x < 1.
Så om vi betraktar för vilka x > 1 som derivatan blir noll så har vi
1 + = 0, som inte har någon lösning.
Om vi betraktar för vilka x som derivatan blir noll så har vi
-1 + = 0.
Hoppas att detta hjälper dig vidare.
tack för att du läser det man skriver och förklara så man förstår, nu kunde jag lösa den
tack för hjälpen!




