Derivera styckvis definierad signal
Hej, till uppgiften nedan vill jag ta fram derivatan till f(t). Är osäker om jag har gjort rätt. Undrar om någon kan se något fel med min beräkning?
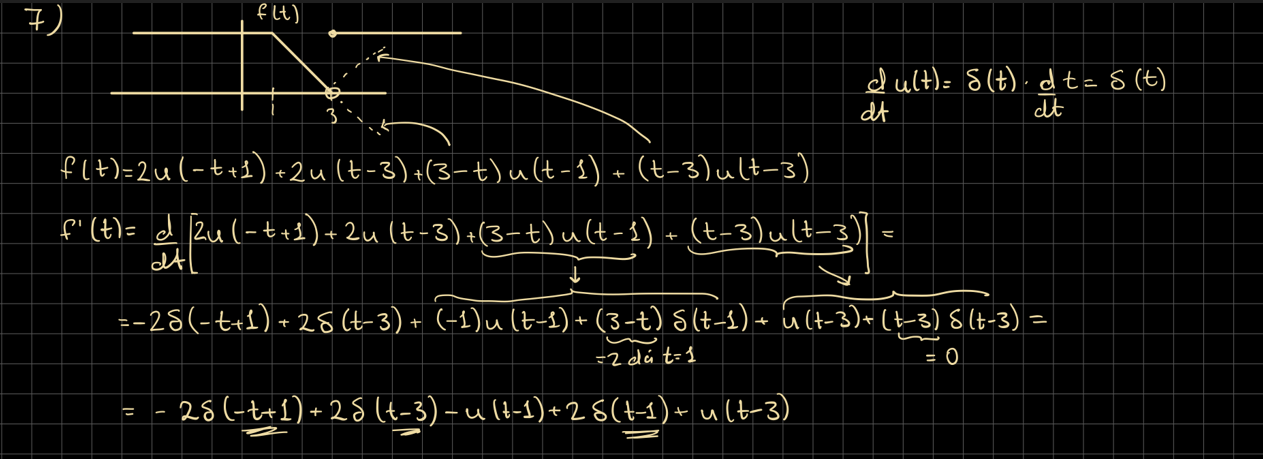
Jag har inte sysslat mycket med detta och det var decennier sedan.
Derivatan är stabilt noll från t = minus oändl till 1, sedan f’(t) = –1 för 1 < t < 3. Sedan gör den ett jättehopp vid t = 3 och fortsätter som 0 åt höger.
Ritar man u(t–1), u(t–3) och d(t–3) (d är delta) och pusslar så ser man att u(t–1) och
u(t–3) bör ha olika tecken för t > 3. Mellan 1 och 3 är u(t–3) = 0 så vi sätter minus framför
u(t–1).
Det ger –u(t–1)+u(t–3)
Då har vi hoppet vid t = 3 kvar. f(t) hoppar från 0 till 2, det kanske ger att derivatan är
2d(t-3), det är här jag känner mig minst säker. Ett hopp från noll till 1 ger derivatan d(t–3), så dubbelt så högt hopp är 2d(t–3), varför inte?
Mitt svar är alltså alternativ 3.
Cien skrev:Hej, till uppgiften nedan vill jag ta fram derivatan till f(t). Är osäker om jag har gjort rätt. Undrar om någon kan se något fel med min beräkning?
Det är inget fel i din uträkning - den är omständlig, men inte fel. Tänk bara på att och är exakt samma (tempererade) distribution, så och tar ut varandra. På så sätt kommer du fram till alternativet 3, precis som Marilyn.
LuMa07 skrev:Cien skrev:Hej, till uppgiften nedan vill jag ta fram derivatan till f(t). Är osäker om jag har gjort rätt. Undrar om någon kan se något fel med min beräkning?
Det är inget fel i din uträkning - den är omständlig, men inte fel. Tänk bara på att och är exakt samma (tempererade) distribution, så och tar ut varandra. På så sätt kommer du fram till alternativet 3, precis som Marilyn.
Tack. På vilket sätt är uträkningen omständlig? Man bör väl uttrycka f(t) som jag har gjort så man slipper att uttrycka intervallen?
Cien skrev:Tack. På vilket sätt är uträkningen omständlig? Man bör väl uttrycka f(t) som jag har gjort så man slipper att uttrycka intervallen?
Man behöver inte uttrycka signalen med en enda formel med flera stegfunktioner utan det räcker att derivera den på varje av intervallen enligt den styckvisa definitionen och i brytpunkterna (d.v.s. och ) behöver man lägga till en puls ifall funktionen hoppar. (Det är i stort sett det Marilyn föreslagit i #2)
så
Eftersom funktionen hoppar med två steg uppåt när , så tillkommer .
Därmed är .

