Derivera tal
Hej!
Fasnat på en uppgift som lyder
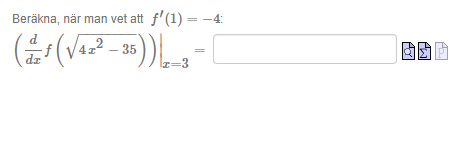
Jag tänker att man ska använda kedjeregeln för inre och yttre derivata men kan inte riktigt komma på hur jag ska börja?
Yttre funktion f(sqrt(x)) och inre funktion 4x^2-35 tror jag det ska vara men osäker.
Behöver en liten kickstart.
Hej Juckeyy och välkommen till pluggakuten!
låt . Vi kan nu notera en bra sak, g(3) blir något som bör göra dig glad, varför?
Beräkna sedan
Den sökta derivatan är nu .
Lätt som en plätt! :)
Guggle skrev :Hej Juckeyy och välkommen till pluggakuten!
låt . Vi kan nu notera en bra sak, g(3) blir något som bör göra dig glad, varför?
Beräkna sedan
Den sökta derivatan är nu .
Lätt som en plätt! :)
Tack, insåg sen att min inre funktion g(x) blev sqrt(4x^2-35), fastnade dock på det enklaste steget att skriva om det som du gjorde att vi säker f'(g(3))*g'(3).
Stort tack för hjälpen!
Guggle skrev :Hej Juckeyy och välkommen till pluggakuten!
låt . Vi kan nu notera en bra sak, g(3) blir något som bör göra dig glad, varför?
Beräkna sedan
Den sökta derivatan är nu .
Lätt som en plätt! :)
Jag har även fastnat på derivatan av denna 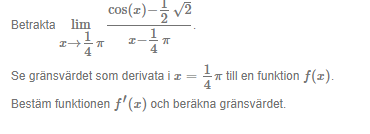
Förstår att kvotregeln inte fungerar men vet inte hur jag ska börja.
Tanken är nog att du ska minnas definitionen av derivata och direkt se att gränsvärdet är lika med derivatan av en viss funktion i en viss punkt.
Bubo skrev :Tanken är nog att du ska minnas definitionen av derivata och direkt se att gränsvärdet är lika med derivatan av en viss funktion i en viss punkt.
Okej förstår. Men jag lyckas inte derivera funktionen.
Gör en ny tråd för varje ny fråga i fortsättningen! Det blir så rörigt annars.
juckeyy skrev :Bubo skrev :Tanken är nog att du ska minnas definitionen av derivata och direkt se att gränsvärdet är lika med derivatan av en viss funktion i en viss punkt.
Okej förstår. Men jag lyckas inte derivera funktionen.
Vad menar du med "funktionen"? Titta på derivatans definition en gång extra.
Bubo skrev :juckeyy skrev :Bubo skrev :Tanken är nog att du ska minnas definitionen av derivata och direkt se att gränsvärdet är lika med derivatan av en viss funktion i en viss punkt.
Okej förstår. Men jag lyckas inte derivera funktionen.
Vad menar du med "funktionen"? Titta på derivatans definition en gång extra.
Om jag ska skriva vad f'(x) så måste ju (cosx-sqrt(2)/2)/(x-(pi/4)) vara det jag ska derivera vilket är f(x)?
Inte alls.
Derivatan av g:
( g(t+h) - g(t) ) / h
Alltså: Skillnaden mellan två funktionsvärden delat med skillnaden mellan x-värdena
Bubo skrev :Inte alls.
Derivatan av g:
( g(t+h) - g(t) ) / h
Alltså: Skillnaden mellan två funktionsvärden delat med skillnaden mellan x-värdena
Ja derivatans definition vet jag hur den ser ut och detta börjar bli pinsamt för min del. Men hur använder jag min ekvation till derivatans definition just här?
Vad har du för skillnad i täljaren? Vad har du för skillnad i nämnaren?
Tips:
tomast80 skrev :Tips:
Pinsamt detta av mig. Men blir det då
(cosx-sqrt(2)/2) - (cosa-sqrt(2)/2) / x-(pi/4)
Menar du att min funktion redan står på formen redo att sätta in bara?
Fan det står helt stilla, jag blir frustrerad och ledsen...
Täljaren:
Roten ur två delat med två är precis det exakta värdet av cos(pi/4).
Nämnaren:
Att x går mot pi/4 är ju samma sak som att skillnaden mellan x och pi/4 går mot noll.
Det är alltid bra att rita en figur.
Här är kurvan cos(x), en punkt (pi/4, cos(pi/4) och en annan punkt på kurvan. Klura nu ut sidorna i den där triangeln.
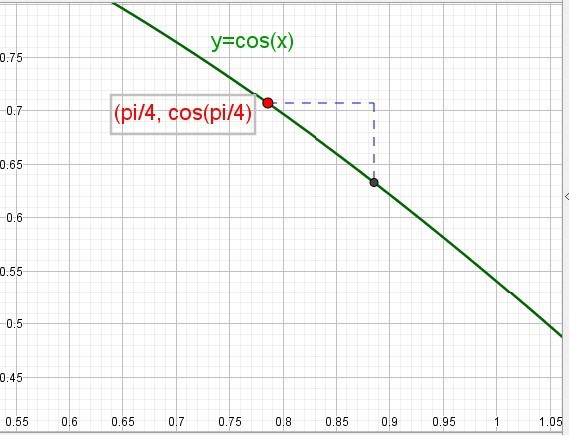
Den "andra punkten" närmar sig (pi/4, cos(pi/4). Vad händer då?
Bubo skrev :Täljaren:
Roten ur två delat med två är precis det exakta värdet av cos(pi/4).
Nämnaren:
Att x går mot pi/4 är ju samma sak som att skillnaden mellan x och pi/4 går mot noll.
Ja roten ur två delar med två vet jag är cospi/4 men om jag ska följa som du skrev innan så blir ju täljaren 0 delar med nämnaren som går mot 0 och då blir det ju 0/0 vilket inte direkt hjälper?
Gränsvärdet är just det som kallas derivata.
juckeyy skrev :Bubo skrev :Täljaren:
Roten ur två delat med två är precis det exakta värdet av cos(pi/4).
Nämnaren:
Att x går mot pi/4 är ju samma sak som att skillnaden mellan x och pi/4 går mot noll.
Ja roten ur två delar med två vet jag är cospi/4 men om jag ska följa som du skrev innan så blir ju täljaren 0 delar med nämnaren som går mot 0 och då blir det ju 0/0 vilket inte direkt hjälper?
Finessen med gränsvärden är just att man inte "kommer fram". Hur nära som helst, men inte ända fram. Då delar man med ett litet tal, men inte med noll.
smaragdalena skrev :Gränsvärdet är just det som kallas derivata.
Ja men 0/0 är ju inte svaret på uppgiften.
Bubo skrev :juckeyy skrev :Bubo skrev :Täljaren:
Roten ur två delat med två är precis det exakta värdet av cos(pi/4).
Nämnaren:
Att x går mot pi/4 är ju samma sak som att skillnaden mellan x och pi/4 går mot noll.
Ja roten ur två delar med två vet jag är cospi/4 men om jag ska följa som du skrev innan så blir ju täljaren 0 delar med nämnaren som går mot 0 och då blir det ju 0/0 vilket inte direkt hjälper?
Finessen med gränsvärden är just att man inte "kommer fram". Hur nära som helst, men inte ända fram. Då delar man med ett litet tal, men inte med noll.
Ja den förståelsen har jag.
Jag vet bara inte hur jag ska lösa denna. Kan någon skriva lösningen så jag kan kolla på den, då tror jag att jag kommer förstå.
Låt vad säger då derivatans definition att om derivatan för i ?
Skriv cos(x) som cos(pi/4+h) och låt h gå mot noll. Vad får du i täljaren? Ser du att nämnaren blir h?




