Deriverbarhet
Hej!
Om en funktion inte är deriverbar i origo, kommer den kunna vara deriverbar för andra x-värden? Men om en funktion inte är deriverbar i ett x värde, kan den vara deriverbar i andra koordinater? Kan någon förklara med hjälp av bilder? Tack
Hej,
Ett bra exempel är funktionen 1/x. Skriv upp den i GeoGebra och kolla ifall den passerar Origo eller inte. Testa även ifall du kan derivera den eller inte.
Ifall den inte är deriverbar i Origo, varför är den inte det då?
Det jag ser är att funktionen kommer aldrig att korsa när x=0. Detta beror på att 0 inte är definierat för nämnaren i det rationella uttrycket då man inte kan dela med ett tal på 0.
Det går väl att derivera funktionen? Jag får att f’(x)=-1/(x^2)
om vi deriverar när x är 0 f’(0)= -1•0^-2
Man kan inte upphöja 0 till ett negativt tal, därför går det ej att derivera.
Dock om vi har f’(-1)= -1•(-1^2)= -1?
Så min slutsats blir nog att det går att derivera att värden än när x=0.
Men om man vill t.ex beskriva dennna funktion med derivata hur gör man då? Man kan inte derivera där grafen har en spets, vid x=-2,828 då detta x värde får olika lutningar när man kommer från vänster och höger. Högra sidan ger ett positivt k värdet medan den vänstra sidan ger ett negativt k värde. Men bågen kan man derivera då den är kontinuerlig samt har inga spetsiga sidor.
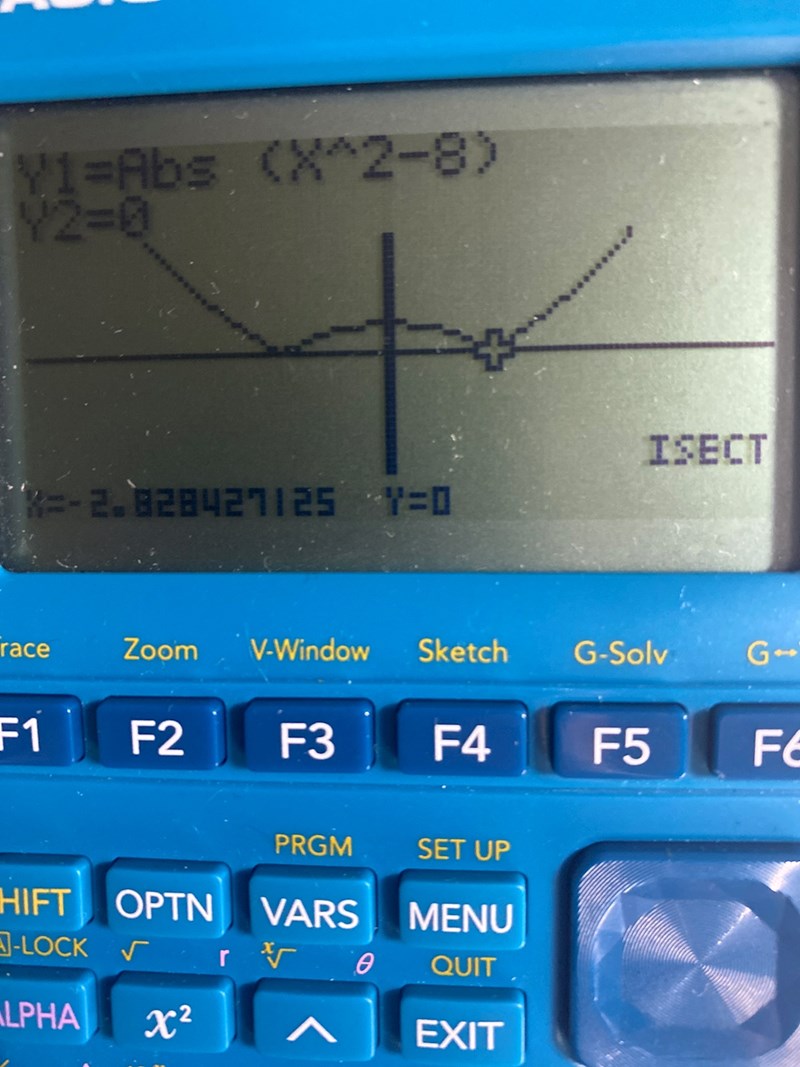
Du får olika derivator i de tre olika intervallen.
Smaragdalena skrev:Du får olika derivator i de tre olika intervallen.
Syftar du på inlägg 3 eller 4 och har jag tänkt rätt?
Det jag skrev i inlägg 3 och 4 är det rätt? För att i första inlägget behövde jag besvara en fråga som jag fick och i mitt andra inlägg ville jag förstå bättre med en annan funktion
Äpple skrev:Smaragdalena skrev:Du får olika derivator i de tre olika intervallen.
Syftar du på inlägg 3 eller 4 och har jag tänkt rätt?
Jag syftade på bilden i #4. Jag ser inga uttryck för derivatan i den bilden, bara en lös reflektion som verkar korrekt.
Det du skriver i #3 begriper jag inte, jag vet inte vilken funktion du syftar på.
Smaragdalena skrev:Äpple skrev:Smaragdalena skrev:Du får olika derivator i de tre olika intervallen.
Syftar du på inlägg 3 eller 4 och har jag tänkt rätt?
Jag syftade på bilden i #4. Jag ser inga uttryck för derivatan i den bilden, bara en lös reflektion som verkar korrekt.
Det du skriver i #3 begriper jag inte, jag vet inte vilken funktion du syftar på.
Det var någon som föreslog i inlägget ovan att jag skulle testa med funktionen 1/x vilket jag skriver om i inlägg 3. Gällande inlägg 4 så fick jag ett absolutbelopp som var |x^2-8| och jag skulle förklara grafens utseende. Hoppas jag förtydligade lite grann
Om du vill derivera f(x) = |x^2-8| : Börja med att ta bort beloppstecknen och dela in funktionen i tre olika intervall. Skriv en funktion för varje intervall. Derivera funktionen i varje intervall.
Alternativt skriver man funktionen som:
och deriverar därefter.
tomast80 skrev:Alternativt skriver man funktionen som:
och deriverar därefter.
ni har missuppfattat allt.. Jag skulle helt enkelt bara skriva in absolutbeloppsfunktionen och förklara grafens utseende. Utifrån grafen kan jag se om vilka x värden är deriverbara eller inte som jag skrev i inlägg 4. Snälla förstår någon?
Äpple skrev:tomast80 skrev:Alternativt skriver man funktionen som:
och deriverar därefter.ni har missuppfattat allt.. Jag skulle helt enkelt bara skriva in absolutbeloppsfunktionen och förklara grafens utseende. Utifrån grafen kan jag se om vilka x värden är deriverbara eller inte som jag skrev i inlägg 4. Snälla förstår någon?
Det du skrev i inlägg #4 är helt rätt.
I inlägg #3 Jag håller med dig att f inte är deriverbar när x=0, men för en annan anledning än de du nämnde i inlägget.
Edit: Om f är odefinierad när x=0 så är f oderiverbar när x=0.
Äpple skrev:Hej!
Om en funktion inte är deriverbar i origo, kommer den kunna vara deriverbar för andra x-värden? Men om en funktion inte är deriverbar i ett x värde, kan den vara deriverbar i andra koordinater? Kan någon förklara med hjälp av bilder? Tack
|x| är inte deriverbar i x=0, inser du varför?
Men |x| är deriverbar överallt på hela R just förutom x=0.
Dracaena skrev:Äpple skrev:Hej!
Om en funktion inte är deriverbar i origo, kommer den kunna vara deriverbar för andra x-värden? Men om en funktion inte är deriverbar i ett x värde, kan den vara deriverbar i andra koordinater? Kan någon förklara med hjälp av bilder? Tack
|x| är inte deriverbar i x=0, inser du varför?
Men |x| är deriverbar överallt på hela R just förutom x=0.
Är det för att om x är 0 inom absolutbeloppet så är det inga steg från origo???
Mohammad Abdalla skrev:Äpple skrev:tomast80 skrev:Alternativt skriver man funktionen som:
och deriverar därefter.ni har missuppfattat allt.. Jag skulle helt enkelt bara skriva in absolutbeloppsfunktionen och förklara grafens utseende. Utifrån grafen kan jag se om vilka x värden är deriverbara eller inte som jag skrev i inlägg 4. Snälla förstår någon?
Det du skrev i inlägg #4 är helt rätt.
I inlägg #3 Jag håller med dig att f inte är deriverbar när x=0, men för en annan anledning än de du nämnde i inlägget.
Edit: Om f är odefinierad när x=0 så är f oderiverbar när x=0.
Ja, men kan man tänka att om man inte kan upphöja 0 med ett annat tal, så kan inte x vara 0, därför är 0 odefinierat i den funktionen?
är det så?




