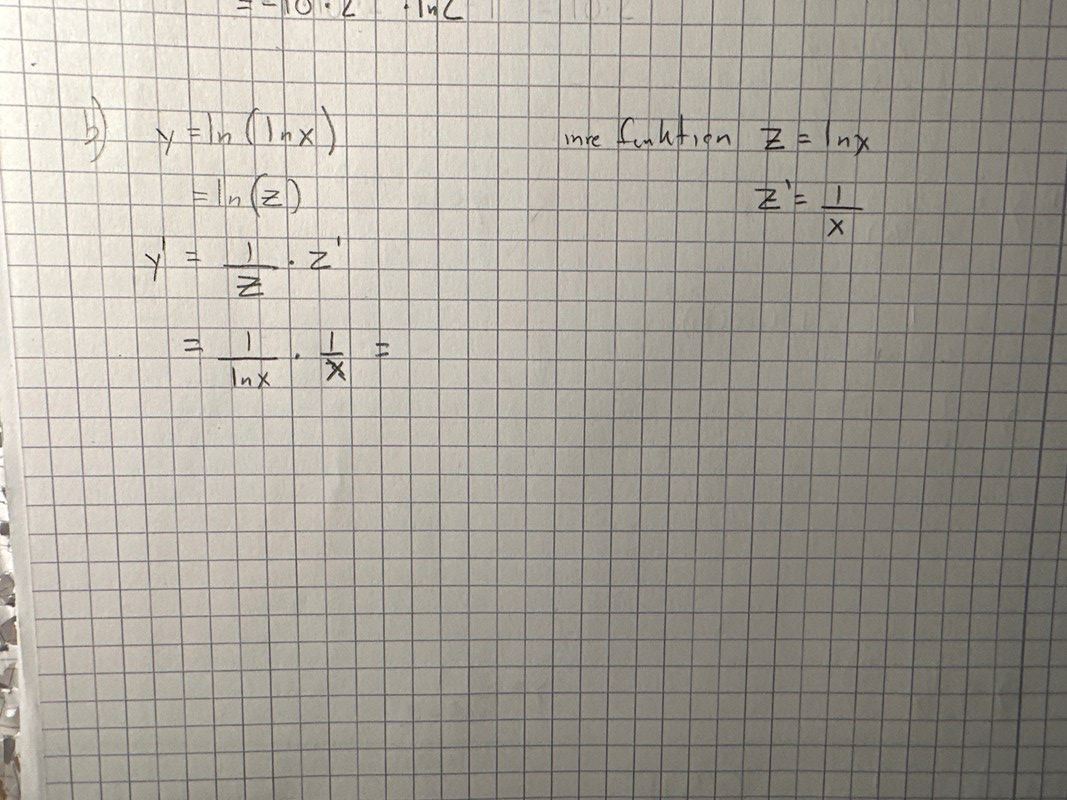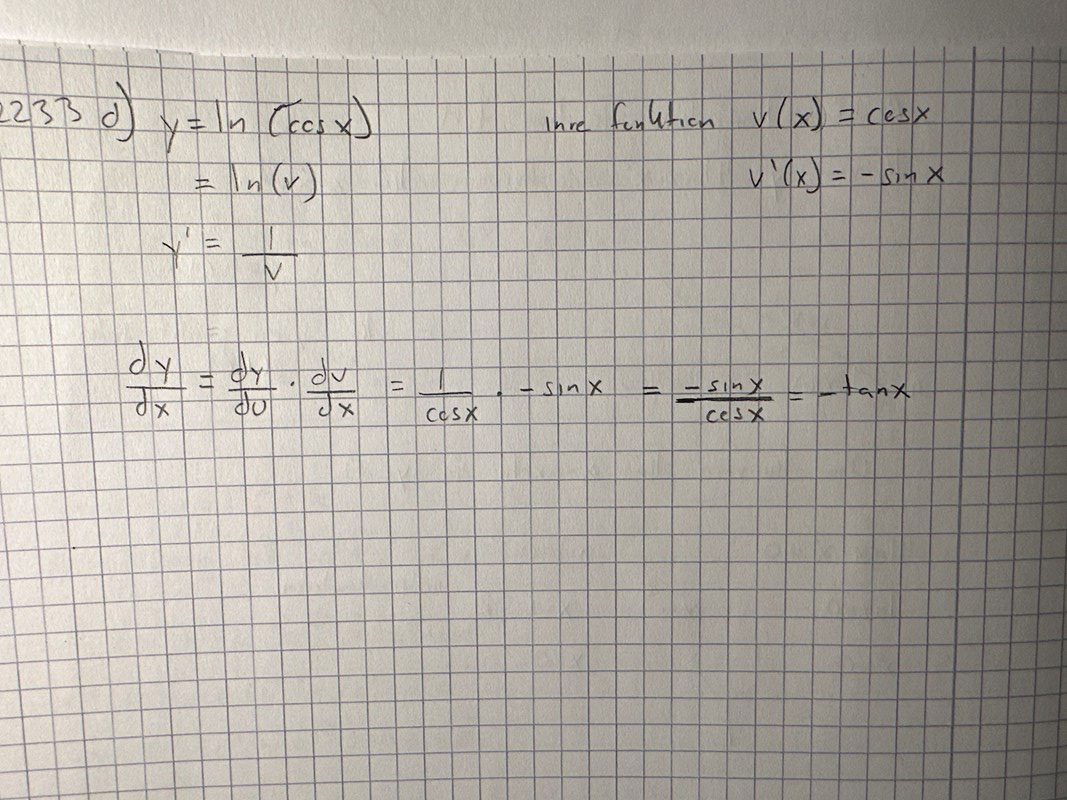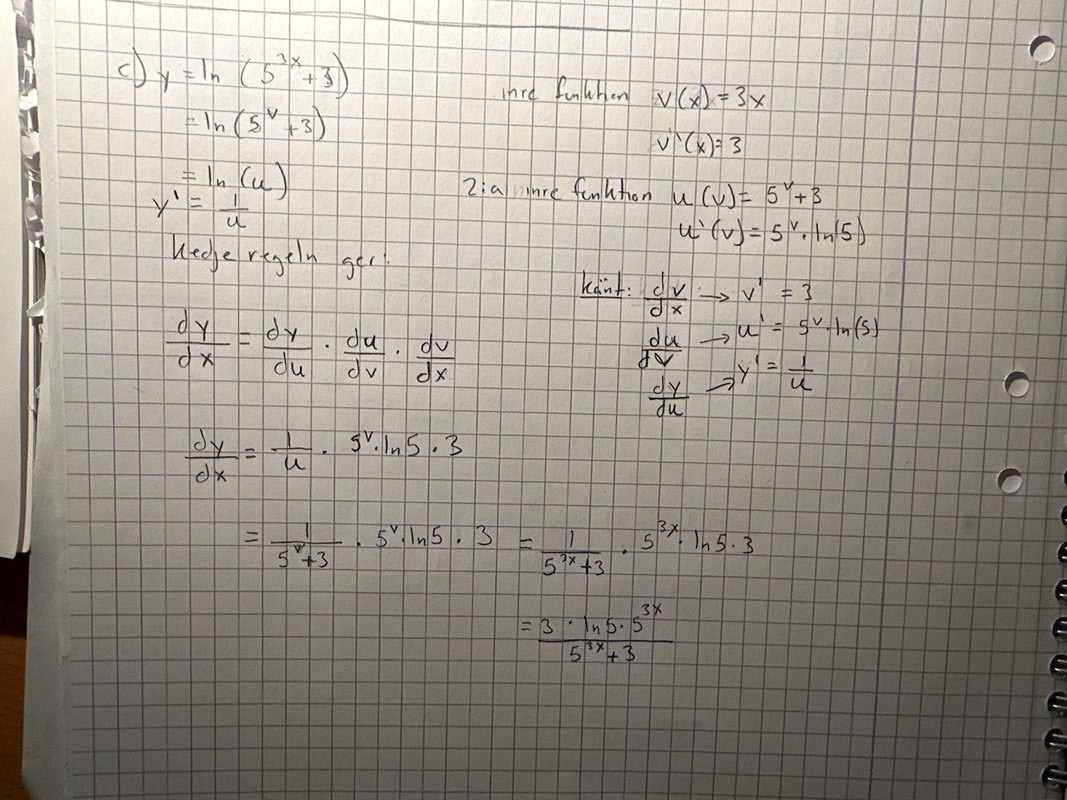Derivering
 hejsan
hejsan
a) ok?

behöver hjälp med b
derivatan av lnx=1/x
Hej.
Ja, a är OK.
För c-uppgiften kan du göra på samma sätt som I a- och b-uppgiften.
Men jag rekommenderar att du byter tillvägagångssätt till följande likartade (samma som jag beskrev i denna tråd):
Utgå från
Sätt , vilket ger dig
Sätt , vilket ger dig
Kedjeregeln ger dig nu
Vi har att
Plocka nu ihop uttrycket för med hjälp av ovanstående.
Det är tydligt att du har förstått hur det fungerar, att du lyckas identifiera inre och yttre funktioner på ett bra sätt och att du kan använda kedjeregeln korrekt. Mycket bra!
Jag vill rekommendera att du genomgående använder dig av skrivsätten , och o.s.v. istället för , och eftersom det då blir tydligare vad det är du deriverar med avseende på.