Derivering av en funktion (med bild)

Hej

$$\begin{gathered} f\left(x\right) kan skrivas som \\ f\left(x\right)=\frac{3}{2}*\frac{1}{x} +{\left(3\right)}^{2x} \\ När man ska derivera {\left(a\right)}^{bx } så blir det b*{\left(a\right)}^{bx }*\ln \left(a\right) \\ {f}^{\text{'}}\left(x\right) =\frac{3}{2}*\frac{-1}{x^2} + 2*3^{2x}*\ln \left(3\right) \\ {f}^{\text{'}}\left(x\right) =\frac{-3}{2x^2} + 2*3^{2x}*\ln \left(3\right) \end{gathered}$$

Polynom deriveras enligt

f(x)=a⋅xⁿ
f′(x)=an⋅xⁿ⁻¹

Kan du skriva om första termen på formen axⁿ ?

Exponentialfunktioner deriveras enligt

f(x)=a^kx har derivatan f′(x)=k⋅lna⋅a^kx

Massa skrev:

Polynom deriveras enligt

f(x)=a⋅xⁿ
f′(x)=an⋅xⁿ⁻¹

Kan du skriva om första termen på formen axⁿ ?

Exponentialfunktioner deriveras enligt

f(x)=a^kx har derivatan f′(x)=k⋅lna⋅a^kx

Löste den på detta sätt: 

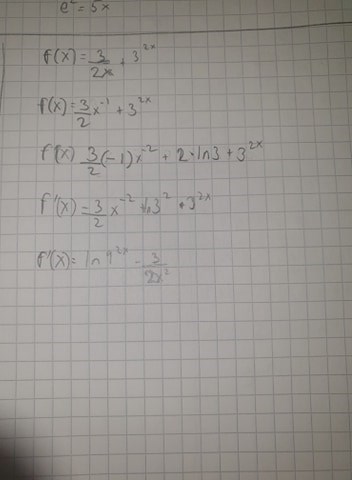
Exp. derivatan blir

2*ln(3)*3^2x det är ej samma sak som 2* ln(3*3^2x)

Den ena av log.lagarna är lg(x⋅y)=lgx+lgy