deriverings fråga

b och c fattar jag hur man löser. C är noll eftersom den går genom origo. För b derivera jag uttrycket till f'(x)=2ax+b. Sedan förstod jag med hjälp av första tangenten att om y=x=0 (origo) att b måste vara 1 för att tangenten ska ha lutningen 1 som y=x har.
Men hur löser man a??
(facit säger att det ska vara 1/12, men det hjälper mig inte mycket)
Den räta linjen har lutningen 2. Var har andragradskurvan lutningen 2?
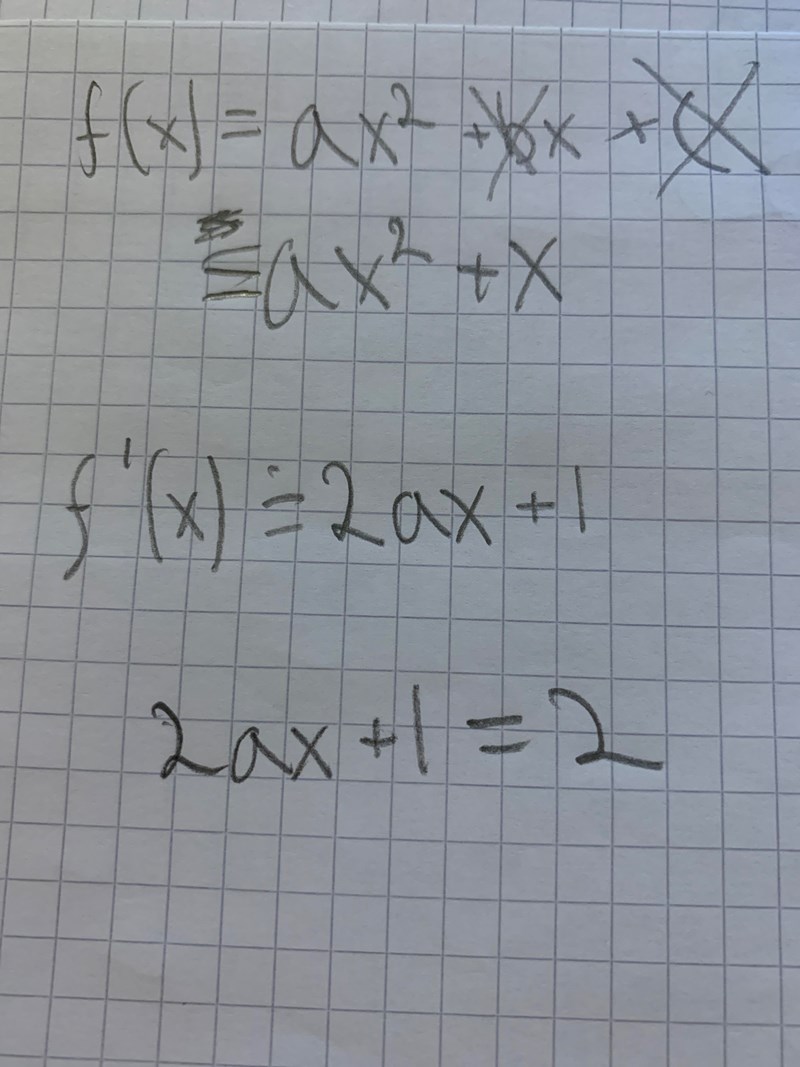 hur ska jag kunna lösa det när det är två variabler? (a och x)
hur ska jag kunna lösa det när det är två variabler? (a och x)
Mackangolf skrev:
hur ska jag kunna lösa det när det är två variabler? (a och x)
Lös ut x som funktion av a. Och tänk på att den räta linjen och andragradskurvan skall tangera varandra för detta värde på x. Vad krävs ytterligare för att så skall vara fallet?
jag vet inte :(
Mackangolf skrev:jag vet inte :(
De två kurvorna måste ha samma y-värde för det x-värde som du fått fram. De kan bara tangera varandra om de går genom samma punkt, eller hur?
PATENTERAMERA skrev:Mackangolf skrev:jag vet inte :(
De två kurvorna måste ha samma y-värde för det x-värde som du fått fram. De kan bara tangera varandra om de går genom samma punkt, eller hur?
Vi har fått fram c = 0 och b = 1, således blir andragradskurvan
y = ax2 + x.
Denna kurva skall tangera y = 2x - 3, som har lutningen 2.
Vi vill således hitta ett x för viket derivatan till andragradsfunktionen är 2, dvs
2ax + 1 = 2, vilket ger
x = 1/(2a).
Kurvan y = ax2 + x och linjen y = 2x - 3 måste ha samma y-värde då x = 1/(2a) (de måste ju gå genom samma punkt för att kunna tangera), vilket ger följande ekvation
a(1/(2a))2 +1/(2a) = 2/(2a) - 3.
Om vi löser denna ekvation får vi a = 1/12.
Har du ritat upp de båda linjerna och det du vet om parabeln?
Tack!


