Deriverings operatorer

Behöver hjälp med en uppgift som handlar om att förenkla ett uttryck så långt som möjligt. Uttrycket är i detta fall rotationen av ett vektorfält v som i sin tur kan beskrivas som ett skalärfält gånger gradienten av ett annat skalärfält. Nedan är bilden på hur långt jag kommit. Min teori är att andra uttrycket i parantesen försvinner p.g.a att partiella derivatorer är kommutativa, men är fast på det första uttrycket.

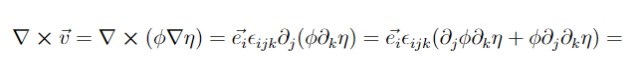
Ja, det är korrekt att den sista termen blir noll. Och den första termen kanske du känner igen om du ser på det så här:

$(\nabla \phi\times\nabla \eta)^i=\varepsilon^{ijk}\frac{\partial \phi}{\partial x^j} \frac{\partial \eta}{\partial x^k}$

D4NIEL skrev:
Ja, det är korrekt att den sista termen blir noll. Och den första termen kanske du känner igen om du ser på det så här:

$(\nabla \phi\times\nabla \eta)^i=\varepsilon^{ijk}\frac{\partial \phi}{\partial x^j} \frac{\partial \eta}{\partial x^k}$

Snyggt! Hade inte tänkt på det där alls! Men då bör svaret sett bara bli grad(phi) x grad(eta) om man lägger till enhetsvektorn och använder summa konventionen?. (2 st i).

Ja, det är ju sambandet (med vektoranalysens indiceringskonvention samt minnesregeln $(\nabla\times\nabla)f=0$ )

$\nabla\times(\phi\nabla \eta)=(\nabla_\phi+\nabla_{\nabla \eta}) \times(\phi\nabla \eta)=\nabla\phi\times \nabla\eta+\phi \nabla\times(\nabla \eta))=\nabla\phi\times \nabla\eta$

Svara

Visa senaste svar