Determinant fråga
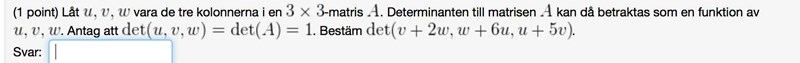
Jag vet inte hur jag måste angripa den här fråga.
I början tänkte jag att motsvarar radoperationer som har inga påverkarn på determinanten. Skillnaden mellan är att vi har introducerat 3 koefficienter.
Så jag trodde svaret var . Som låter lite stor...
Och det blev fel.
Hej Dajamanté
- En determinant ändras ej, om man till elementen i en viss rad eller kolonn adderar elementen från en annan rad respektive kolonn multiplicerade med en konstant c.
- Om alla element i en rad eller kolonn multipliceras med en konstant c så multipliceras determinanten med samma konstant c.
- Om två rader eller kolonner byter plats, så multipliceras determinanten med -1
Kan du genom att använda dessa operationer omvandla (u, v, w) till (v+2w, w+6u, u+5v)?
Isf.. vi har rad som multiplicerades med 2, som multiplicerades med 6 och som multiplicerades med 5.
Inga rader eller kolonn har bytt plats och inga djur blev skadad under inspelningen.
Men tyvärr är inte svaret , som jag redan testade förut...
Jag förstår inte vad du gör.
(u,v,w) -> (v+2w, w+6u, u+5v) kräver mer än några multiplikationer.
Byt plats på kolonn 1 och 2 (det=-1)), byt plats på kolonn 2 och 3 (det =-1*-1=1)
(u,v,w)->(v,w,u), determinanten är fortfarande 1.
Lägg 2 från kolonn 2 till kolonn 1, lägg 6 från kolonn 3 till kolonn två
(v,w,u)->(v+2w, w+6u, u), determinanten är fortfarande 1.
Multiplicera kolonn 3 med 61, determinanten är 61.
Lägg 5 från kolonn1 till kolonn 3, lägg -10 från kolonn 2 till kolonn 3.
(v+2w, w+6u, 61u)->(v+2w, w+6u, u+5v), determinanten är 61.
Jag förstår inte vad duuuu gör!
Varifrån har du dragit ur 61?
Ånej jag fick hjärnblödning -tänkandeolycka-, måste titta på StarWars!!!
(jag skojas, jag ska bara fundera på vad du skrev..)
Men seriöst, 61?
Hej!
Det gäller att bestämma en linjär avbildning () sådan att
och och
Eftersom determinanten så är vektorerna , och linjärt oberoende vilket betyder att de bildar en bas i rummet. Uttryckt i denna bas är vektorn och vektorn samt vektorn Avbildningsmatrisen i denna bas är därför
och Sarrus regel ger dess determinant
Albiki
Du ska bestämma determinanten När du väl bestämt avbildningsmatrisen använder du determinanters multiplikativa egenskap för att få
Det måste jag fundera på ordentligt...
dajamanté skrev :Varifrån har du dragit ur 61?Ånej jag fick hjärnblödning -tänkandeolycka-, måste titta på StarWars!!!
(jag skojas, jag ska bara fundera på vad du skrev..)
Men seriöst, 61?
Du vill plocka ihop a st (v+2w) från kolonn 1, b st (w+6u) från kolonn 2 och c stycken u från kolonn 3 och lägga alltihop i kolonn 3 för att få u+5v. Alltså
.
Ingår linjära avbildningar i er kurs?
Jag är inte säkert på det. Jag ska fråga.
Edit: jag fick en annan tips för hur man löser den, återkommer.....
Guggle skrev :Jag förstår inte vad du gör.
(u,v,w) -> (v+2w, w+6u, u+5v) kräver mer än några multiplikationer.
Byt plats på kolonn 1 och 2 (det=-1)), byt plats på kolonn 2 och 3 (det =-1*-1=1)
(u,v,w)->(v,w,u), determinanten är fortfarande 1.
Lägg 2 från kolonn 2 till kolonn 1, lägg 6 från kolonn 3 till kolonn två
(v,w,u)->(v+2w, w+6u, u), determinanten är fortfarande 1.
Multiplicera kolonn 3 med 61, determinanten är 61.
Lägg 5 från kolonn1 till kolonn 3, lägg -10 från kolonn 2 till kolonn 3.
(v+2w, w+6u, 61u)->(v+2w, w+6u, u+5v), determinanten är 61.
Hej igen Guggle,
Jag förstår fortfarande inte hur du gör, tipsen jag fick var så där:
Skriva den första matrisen (efter har bytt raderna) och sedan en ny tomt matris för att hitta rätt koefficienterna.
Typ så här:
Och därifrån titta hur många som behövdes för att få resultat matris. Första kolonnen blir då 1, 2, 0. Andra blir 0, 1, 6 och den sista bli 5, 0, 1.
Determinanten på detta matris blir 61. Läraren nämnde inte radbyten (varför inte?)
Är det det du försökte förklara för mig? Din lösning ser enklare ut. Hur bestämmer du att bara lägga tal till olika kolonner?
dajamanté skrev :Multiplicera kolonn 3 med 61, determinanten är 61.
Lägg 5 från kolonn1 till kolonn 3, lägg -10 från kolonn 2 till kolonn 3.
(v+2w, w+6u, 61u)->(v+2w, w+6u, u+5v), determinanten är 61.
Hej igen Guggle,
Jag förstår fortfarande inte hur du gör, tipsen jag fick var så där:
Skriva den första matrisen (efter har bytt raderna) och sedan en ny tomt matris för att hitta rätt koefficienterna.
Hej Daja, den första lösningsmetoden använder de grundläggande räknelagarna för determinanter för att ordna om determinanten till det vi söker. Ungefär som när man gör elementära radoperationer på en matris kan man göra elementära operationer på en determinant (byta plats, addera kolonner, multiplicera med konstanter osv).
Genom att byta plats på- , addera och multiplicera kolonner omformar jag determinanten till det som eftersöks.
Den andra lösningsmetoden (som du fick tips om) bygger på att man först undersöker hur man transformerar matrisen A till det man vill ha (M) genom att multiplicera med en annan matris (P) från höger . Man konstruerar P så att M=AP. Sedan beräknas determinanten för P och slutligen använder man multiplikationssatsen för determinanter det(M)=det(AP)=(det A)(det P).
Denna metod är ungefär samma sak som att definiera en linjär avbildning F som avbildar de "gamla" basvektorerna (u,v,w) på de "nya" (v+2w, w+6u, u+5v).
Matrisen för F i basen är
Determinanten av M ges av det(T) det(A)
Detta definierar alltså matrisrepresentationen av sambandet , där x och y är koordinatvektorer. Men det är inte riktigt så rättframt som det framstår och om du inte läst om linjära avbildningar samt känner till och kan bevisa multiplikationssatsen för determinanter tycker jag att det är en lite överkurs-lösning.
Determinanten på detta matris blir 61. Läraren nämnde inte radbyten (varför inte?)
Du behöver inte byta rader i metod två, det går utmärkt att ta fram en matris som kan multipliceras från höger och ge den transformerade matris du vill ha redan från början.
Vad som däremot är viktigt att påpeka är att när två kolonner byter plats multipliceras determinanten med -1. Du byter plats två gånger vilket ger (-1 * -1=1) så det råkar inte spela någon roll i just det här fallet. Men självklart måste man känna till och nämna det i sin lösning.
Jag känner att detta mening...
Multiplicera kolonn 3 med 61, determinanten är 61.
... kommer att spöka mig länge.
Men okej då, så länge kan jag släpa det. Har prov imorgon, dessutom nu ska vi börja cross product, och jag blev ganska upprörd som vanligt (=fyfan, jag fattar ingenting, hjälp, vad är det som pågår) av att skimma igenom kompendiet och matteboken som vanligt.



