Diagnos 3. Uppgift 4 a). Matematik 5000.
Hej,
Hur löser man den här uppgiften för a)?
Jag satte 12(cosx + sinx) och sedan deriverade till (sinx-cosx) som är då 45°. Men det är fel..
Det hjälper om man deriverar rätt kanske:p
Typ till -sin(x) - cos(x)
Eller nej det blir konstigt

Jag hade provat med
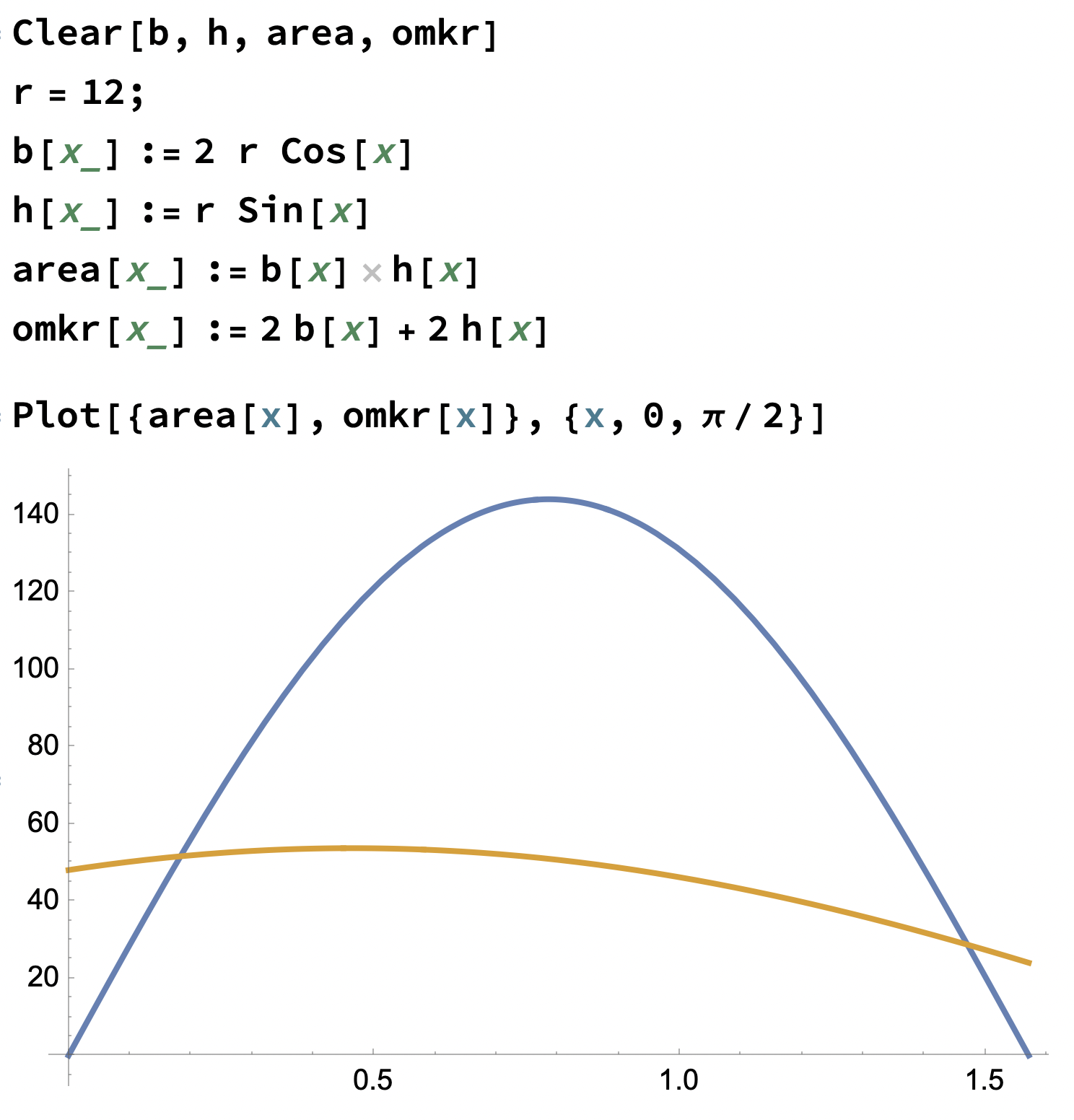
Måste det lösas med verktyg eller hur menar du.
Eller det går att göra utifrån cirkelns ekvation x^2+y^2 = 144, lösa för y och sedan sätta in i ett uttryck för omkretsen och ta det därifrån. Uh
Dkcre skrev:Eller det går att göra utifrån cirkelns ekvation x^2+y^2 = 144, lösa för y och sedan sätta in i ett uttryck för omkretsen och ta det därifrån. Uh
Du kan göra båda. Antingen använder du x^2+y^2=12^2 eller så använder du sin och cos. Det är en smaksak.
Går att göra för hand. Jag bara visade på lite idéer om beteckningar och sedan graferna som visar på max.
Jag gillar trig funktionerna generellt, av någon anledning. Men då är det verktyg som gäller?
Dkcre skrev:Jag gillar trig funktionerna generellt, av någon anledning. Men då är det verktyg som gäller?
För hand.
Det kan jag inte. Eller jag måste ha med konstanten och derivera den med kanske.
Eller jag har ju blandat ihop derivata och primitiv funktion och allt möjligt ser jag.. därför det inte går.
Tror jag grejar det
Nej, jag kunde inte. Kan inte längre än det här.
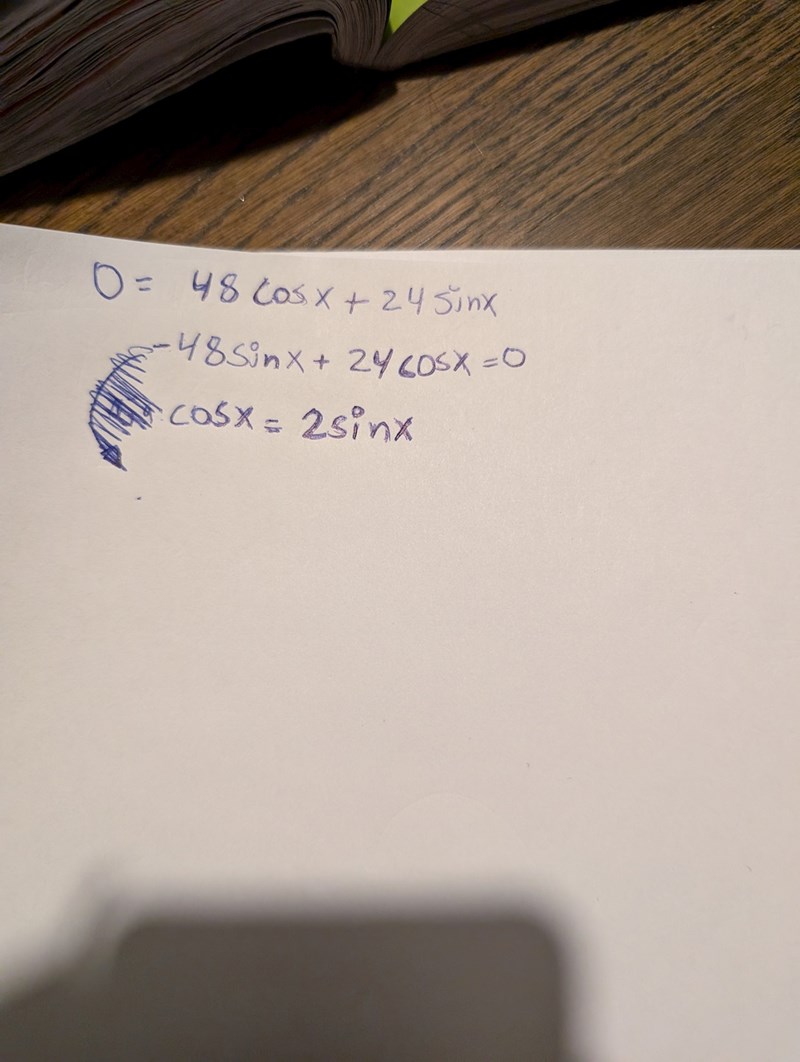
Råkade du inte få precis det här svaret i en helt annan uppgift nyligen? Det kanske var någon annan.
Om du skriver om lite så får du
sin(x)/cos(x) = 1/2
Visa spoiler

Okej tack tack



