Diagrammet visar hennes hastighet som en funktion av tiden. Bestäm v’(120)

Hej.

har lite svårt att tolka denna. Jag ser inget funktionsuttryck för v som indikerar att detta är grafen till just v. Det faktum att y i grafen som indikerar hastigheten m/s tolkar jag som att detta är derivatan över tid. Men menar de typ andraderivatan i det här fallet med v’(120) eller att v(t) är sträckan Elin färdats efter t sekunder?

vi har inte gått igenom andraderivatan i boken ännu eller något annat förutom derivatans definition. Inte kollat i facit ännu för vill förstå vad det är jag missuppfattar först.

mvh

Det står inte uttryckligen, men v brukar betyda hastighet ( v som i velocity).

Nehepp. Gissade fel. De menar alltså andraderivatan av den ursprungliga (primitiva?) funktionen? Lite så jag tolkar det.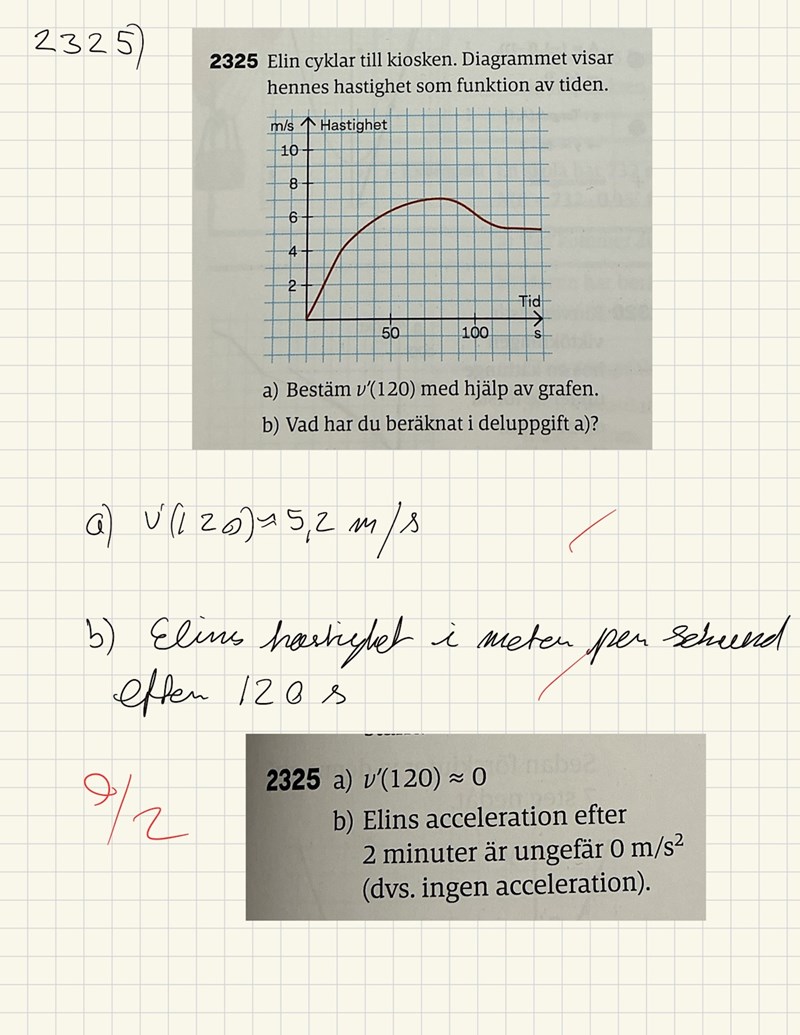

Deriverar du hastighet med avseende på tid får du acceleration: dv/dt. Skillnaden i hastighet över tid.

v’(120) är alltså accelerationen vid tiden t=120. Jag skulle ta en linjal och dra en linje i diagrammet. Sedan är lutningen av tangenten din acceleration.

Verkar det rimligt?

PS. Tänk på enheten i svaret.

sictransit skrev:
Deriverar du hastighet med avseende på tid får du acceleration: dv/dt. Skillnaden i hastighet över tid.

v’(120) är alltså accelerationen vid tiden t=120. Jag skulle ta en linjal och dra en linje i diagrammet. Sedan är lutningen av tangenten din acceleration.

Verkar det rimligt?

PS. Tänk på enheten i svaret.

Spännande.. intressant att de tar upp detta vid intro av derivata. Lite random.

antar att enheten blir m/s^2? Ja, precis. Såg det nu i facit. Tror jag stött på en liknande uppgift där enheten var samma och då fick jag tänka till innan jag förstod.:)

tack för svaret. Lägger definitivt det på minnet.

maratmatorkin skrev:
sictransit skrev:
Deriverar du hastighet med avseende på tid får du acceleration: dv/dt. Skillnaden i hastighet över tid.

v’(120) är alltså accelerationen vid tiden t=120. Jag skulle ta en linjal och dra en linje i diagrammet. Sedan är lutningen av tangenten din acceleration.

Verkar det rimligt?

PS. Tänk på enheten i svaret.

Spännande.. intressant att de tar upp detta vid intro av derivata. Lite random.

antar att enheten blir m/s^2? Ja, precis. Såg det nu i facit. Tror jag stött på en liknande uppgift där enheten var samma och då fick jag tänka till innan jag förstod.:)

tack för svaret. Lägger definitivt det på minnet.

Det är en ganska bra intro. När man kommer till derivata i matten, så har man ju redan pysslat en del med sträcka, hastighet och acceleration i fysiken.

Du känner säkert igen den här, sträckan givet utgångshastighet och acceleration över tid:

$s = s_{0} + v_{0} t + \frac{a t^{2}}{2}$

Vad får vi om vi deriverar sträckan med avseende på tid?

$s' = \frac{d s}{d t} = v = v_{0} + \frac{a \times 2 t^{1}}{2} = v_{0} + a t$

Hastigheten vid tiden t beror alltså på utgångshastigheten v₀ plus accelerationen a gånger tiden t. Rimligt!

Eller åt andra hållet, med primitiva funktioner:

Du accelererar med accelerationen a. Vilken hastighet har du då vid tiden t?

Vi sätter f(t)=a, alltså med en konstant acceleration oberoende av tid.

Den primitiva funktionen blir:

$F (t) = a t + C$

Här är F(t) din hastighet över tid. Konstanten C är ditt v₀.

Hur långt har vi kommit då?

Ja, vi sätter $g (t) = a t + C$ .

Då får vi: $G (t) = \frac{a t^{2}}{2} + C t + D$

G(t) är din sträcka. C var v₀ och den nya konstanten D är ditt s₀.

Det är så lätt att matten bara blir abstrakt. Man deriverar (eller integrerar) utan att tänka på att man redan hållit på med det här i fysiken.

sictransit skrev:
maratmatorkin skrev:
sictransit skrev:
Deriverar du hastighet med avseende på tid får du acceleration: dv/dt. Skillnaden i hastighet över tid.

v’(120) är alltså accelerationen vid tiden t=120. Jag skulle ta en linjal och dra en linje i diagrammet. Sedan är lutningen av tangenten din acceleration.

Verkar det rimligt?

PS. Tänk på enheten i svaret.

Spännande.. intressant att de tar upp detta vid intro av derivata. Lite random.

antar att enheten blir m/s^2? Ja, precis. Såg det nu i facit. Tror jag stött på en liknande uppgift där enheten var samma och då fick jag tänka till innan jag förstod.:)

tack för svaret. Lägger definitivt det på minnet.

Det är en ganska bra intro. När man kommer till derivata i matten, så har man ju redan pysslat en del med sträcka, hastighet och acceleration i fysiken.

Du känner säkert igen den här, sträckan givet utgångshastighet och acceleration över tid:

$s = s_{0} + v_{0} t + \frac{a t^{2}}{2}$

Vad får vi om vi deriverar sträckan med avseende på tid?

$s' = \frac{d s}{d t} = v = v_{0} + \frac{a \times 2 t^{1}}{2} = v_{0} + a t$

Hastigheten vid tiden t beror alltså på utgångshastigheten v₀ plus accelerationen a gånger tiden t. Rimligt!

Eller åt andra hållet, med primitiva funktioner:

Du accelererar med accelerationen a. Vilken hastighet har du då vid tiden t?

Vi sätter f(t)=a, alltså med en konstant acceleration oberoende av tid.

Den primitiva funktionen blir:

$F (t) = a t + C$

Här är F(t) din hastighet över tid. Konstanten C är ditt v₀.

Hur långt har vi kommit då?

Ja, vi sätter $g (t) = a t + C$ .

Då får vi: $G (t) = \frac{a t^{2}}{2} + C t + D$

G(t) är din sträcka. C var v₀ och den nya konstanten D är ditt s₀.

Det är så lätt att matten bara blir abstrakt. Man deriverar (eller integrerar) utan att tänka på att man redan hållit på med det här i fysiken.

Tack för svaret! Läser igenom noggrannare när jag påbörjat min dag efter morgonrutinen. :)

sictransit skrev:
maratmatorkin skrev:
sictransit skrev:
Deriverar du hastighet med avseende på tid får du acceleration: dv/dt. Skillnaden i hastighet över tid.

v’(120) är alltså accelerationen vid tiden t=120. Jag skulle ta en linjal och dra en linje i diagrammet. Sedan är lutningen av tangenten din acceleration.

Verkar det rimligt?

PS. Tänk på enheten i svaret.

Spännande.. intressant att de tar upp detta vid intro av derivata. Lite random.

antar att enheten blir m/s^2? Ja, precis. Såg det nu i facit. Tror jag stött på en liknande uppgift där enheten var samma och då fick jag tänka till innan jag förstod.:)

tack för svaret. Lägger definitivt det på minnet.

Det är en ganska bra intro. När man kommer till derivata i matten, så har man ju redan pysslat en del med sträcka, hastighet och acceleration i fysiken.

Du känner säkert igen den här, sträckan givet utgångshastighet och acceleration över tid:

$s = s_{0} + v_{0} t + \frac{a t^{2}}{2}$

Vad får vi om vi deriverar sträckan med avseende på tid?

$s' = \frac{d s}{d t} = v = v_{0} + \frac{a \times 2 t^{1}}{2} = v_{0} + a t$

Hastigheten vid tiden t beror alltså på utgångshastigheten v₀ plus accelerationen a gånger tiden t. Rimligt!

Eller åt andra hållet, med primitiva funktioner:

Du accelererar med accelerationen a. Vilken hastighet har du då vid tiden t?

Vi sätter f(t)=a, alltså med en konstant acceleration oberoende av tid.

Den primitiva funktionen blir:

$F (t) = a t + C$

Här är F(t) din hastighet över tid. Konstanten C är ditt v₀.

Hur långt har vi kommit då?

Ja, vi sätter $g (t) = a t + C$ .

Då får vi: $G (t) = \frac{a t^{2}}{2} + C t + D$

G(t) är din sträcka. C var v₀ och den nya konstanten D är ditt s₀.

Det är så lätt att matten bara blir abstrakt. Man deriverar (eller integrerar) utan att tänka på att man redan hållit på med det här i fysiken.

Hmm. Det här blev lite mycket dock då jag aldrig läst fysik (gick sam-juridik för många många år sedan). Förstod lite halvt men inte mer. Får ta det när jag börjar med den förhoppningsvis nästa år.

Svara

Visa senaste svar