1
svar
157
visningar
diff ekvation med sin(2x)
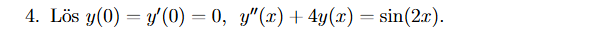 Jag har provat att göra ansatsen y=ze^(2ix) och sedan derivera y osv. jag får fram en partikulär lösning men det blir fel svar. gäller det att om y(0)=y'(0)=0 så är y homogen = 0 ?
Jag har provat att göra ansatsen y=ze^(2ix) och sedan derivera y osv. jag får fram en partikulär lösning men det blir fel svar. gäller det att om y(0)=y'(0)=0 så är y homogen = 0 ?
Kan du visa vad du gjort?
Ansatsen funkar bra. Det är bara att man deriverar rätt enligt produkt- respektive kedjeregeln.
Även om , så kan man inte direkt dra slutsatsen att den homogena lösningen är . Den partikulära lösningen påverkar vilka konstanter som fås utifrån begynnelsevillkoren.
Hitta en allmän lösning (d.v.s. homogen + partikulär) först och sedan får du sätta in i den funna lösningen och dess derivata för att därefter lösa ut konstanterna i lösningen ur ekvationerna respektive .

