Diffekvation

Det finns ingen lösning på den formen. Däremot stämmer inte din förenkling här: 

Andreas Wartel skrev:

Men om $k$ är $-\frac{1}{2x}$ så är $y=e^{-\frac{1}{2x}x}=e^{-\frac{1}{2}}$

Detta stämmer endast om x är nollskild. 

Det finns lösningar, men de är på formen $y\left(x\right)=C{e}^{\frac{x^2}{4}}$, och andra lösningsmetoder. :)

EDIT: Se Lagunas inlägg längre ned i tråden. 

Ok tack! Ja uppgiften handlar egentligen om att avgöra om tangenter som markerats i ett riktingsfält lutar rätt. 

Men jag förstår inte hur jag skulle derivera eller så att säga derivera baklänges för att komma fram till $Ce\frac{x^2}{4}$. Om vi börjar med hur man skulle derivera $Ce\frac{x^2}{4}$, vad är $k$? jag blir förvirrad av $x^2$-termen. Är det en sammansatt funktion?

Ursäkta om det ser otydligt ut. x^2/4 är en exponent. :)

EDIT: Se Lagunas inlägg längre ned i tråden. 

Jo jag tror vi menar samma. Men förstår inte riktigt hur jag kan derivera detta. Alltså uppgiften går ut på att jag genom att få veta att y´=−y/2x ska se att derivatan i punkten (2, 2) ska vara -1/2. Hur kan jag komma fram till y?

Tror jag fattar nu. Behöver väl inte ens hitta f(x). Jag sätter ju y=2 och x=2. Då står det ju y’=-1/2, tänk va!

Om det är tangentlinjerna du ska kontrollera, så räcker det absolut, ja! :)

Jag tror inte lösningsmetoden är för avancerad för Matte 5. Så här gör man:

y'/y = -1/2x = -1/2 * 1/x

ln(y) = -1/2 * ln(x) + C₁ 

y = C * x^-1/2 = $\frac{C}{\sqrt{x}}$

Laguna skrev:

Jag tror inte lösningsmetoden är för avancerad för Matte 5. Så här gör man:

y'/y = -1/2x = -1/2 * 1/x

ln(y) = -1/2 * ln(x) + C₁ 

y = C * x^-1/2 = $\frac{C}{\sqrt{x}}$

Helt rätt, gissa vem som glömde en parentes? 😅

Tack! Men jag är fortfarande nybörjare i differentialekvationer och försöker förstå det mest basala. Man skriver i min lärobok att y´=2y och så har de ritat ett riktningsfält där man tex kan se att när y=1 så lutar tangenterna med k=2. Detta är inte svårt att förstå. Men så skriver de att just denna ekvation kan lösas exakt: $y=Ce^{2x}$. Det jag inte förstår är att om jag är fri att välja $C$ så kan jag ju få vilket värde som helt. Menar man att om man tex sätter x=7347 och hittar ett C så att $y=Ce^{2·7347}=1$, så har man hittat en lösningskurva?

Jag är inte säker på hur du menar, men ett vektorfält innehåller olika värden på C. Denna bild (snodd från WolframAlpha) visar just 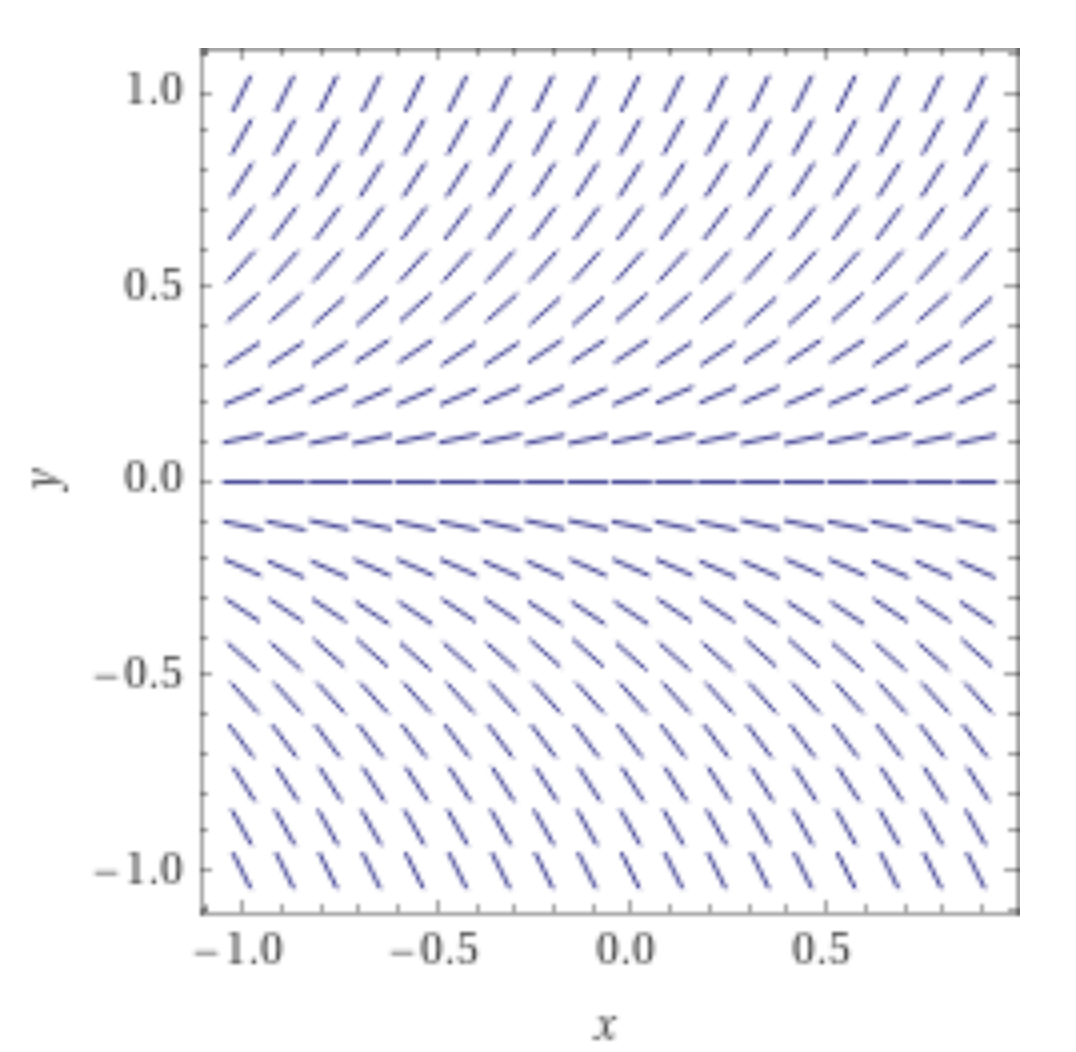$y'=2y$:

Här kan vi hitta många olika kurvor, alla på formen $y=Ce^{2x}$: 

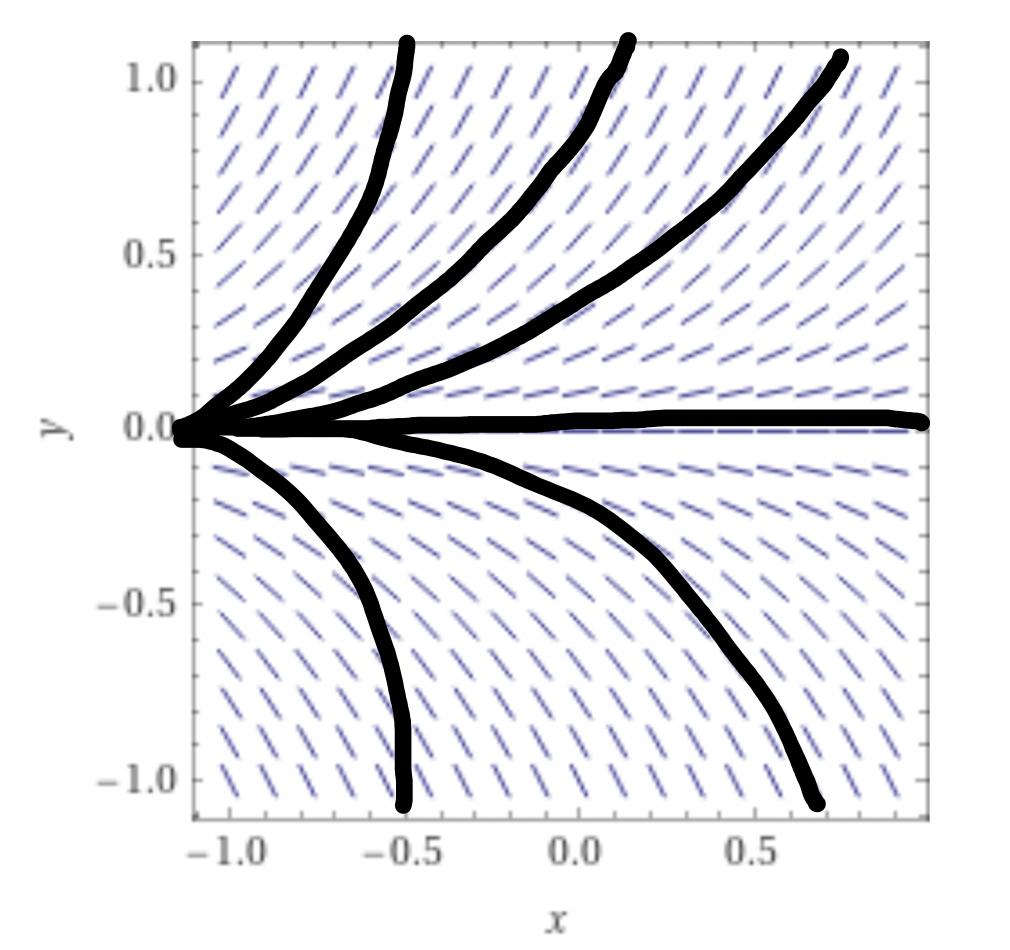
Varje svart linje motsvarar $y=Ce^{2x}$ för ett visst värde på C. :)