Differentialekvation för ström

Det ser rätt ut, förutom att du skrivit fel i sista uttrycket "R2*i'(t)". Det ska vara "R2*i(t)"

Sen finns det ett samband mellan strömmen i och laddningen q som gör att du kan skriva detta som en differentialekvation i endast funktionen q(t).

Mega7853 skrev:

Det ser rätt ut, förutom att du skrivit fel i sista uttrycket "R2*i'(t)". Det ska vara "R2*i(t)"

Sen finns det ett samband mellan strömmen i och laddningen q som gör att du kan skriva detta som en differentialekvation i endast funktionen q(t).

Tack för svar!

Jag har skrivit detta samband nu: 

$L\times \frac{di\left(t\right)}{d\left(t\right)} + (R_1+R_2) * i\left(t\right)\frac{1}{C} = u\left(t\right)$

Jag vill sedan dock skriva om sambandet såhär men misstänker att jag kan gjort fel. : 

$i\text{'}\left(t\right) + 70i\left(t\right) + 2q\left(t\right) = 19\cos \left(10t\right)$

Denna har jag sedan deriverat till: 

$i\text{'}\text{'}\left(t\right) + 70i\text{'}\left(t\right) + 2i\left(t\right) = -190\sin 10t$

Du ska inte skriva ekvationen i funktionen i(t), utan i funktionen q(t). Sedan kan du dividera bort L som du gjort på andra raden.

$$\begin{gathered} i=\frac{dq}{dt} \\ i\text{'}=\frac{d^{2}q}{d{t}^2} \end{gathered}$$

Mega7853 skrev:

Du ska inte skriva ekvationen i funktionen i(t), utan i funktionen q(t). Sedan kan du dividera bort L som du gjort på andra raden.

$$\begin{gathered} i=\frac{dq}{dt} \\ i\text{'}=\frac{d^{2}q}{d{t}^2} \end{gathered}$$

Nu hänger jag inte riktigt med. Vad menar du? 

Det verkar som att du har försöka skriva ekvationen i funktionen i(t) och när du kom till q(t) så deriverade du q(t) för få i(t).

Men du ska istället skriva ekvationen i q(t) och skriva om i(t) som q'(t) och i'(t) som q''(t).

Mega7853 skrev:

Det verkar som att du har försöka skriva ekvationen i funktionen i(t) och när du kom till q(t) så deriverade du q(t) för få i(t).

Men du ska istället skriva ekvationen i q(t) och skriva om i(t) som q'(t) och i'(t) som q''(t).

Ja precis, men det gör jag eftersom att q'(t) = i(t), som jag skrev i inledningen. Jag vill ha ekvationen i i(t) eftersom att jag inte kan jobba med q(t) utifrån de verktyg jag har och eftersom att programmet ska köras i Matlab. 

Ok. Det var inte klart för mig att du inte kan använda q(t). Annars brukar man lösa i q(t) och få ut strömmen i(t) som q'(t).

Så din fråga gäller egentligen om det är tillåtet att derivera båda sidor av en ekvation? Det är generellt inte tillåtet. Det finns fall där det fungerar, men jag kan för lite om detta för att svara på den frågan.

Mega7853 skrev:

Ok. Det var inte klart för mig att du inte kan använda q(t). Annars brukar man lösa i q(t) och få ut strömmen i(t) som q'(t).

Så din fråga gäller egentligen om det är tillåtet att derivera båda sidor av en ekvation? Det är generellt inte tillåtet. Det finns fall där det fungerar, men jag kan för lite om detta för att svara på den frågan.

Nej precis. Har försökt följa utifrån hur vi gör på universitet. Här är ett exempel på hur min professor gjort i ett exempel: 

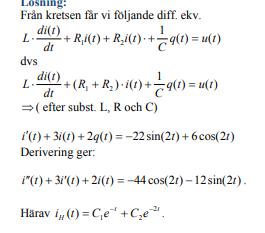
Då ser det ut som att det är tillåtet när ekvationen ser ut på det sättet. Då är det bara att köra på, precis som du har gjort.

Nu när jag tittar lite noggrannare så verkar du har skrivit fel på koefficienten till q(t) (eller i(t) efter derivering). Du har skrivit 2, men det ska väl vara 1/C = 1/0.001 = 1000?

Sen står det (15+a) i uttrycket för u(t), men du har förenklat till 19.

Om jag skulle skriva det så skulle det bli

$L\frac{di}{d{t}^{}}+(R_1+R_2)i+\frac{q}{C}=(15+a)\cos \left(10t\right)$

och sedan efter derivering

$L\frac{d^{2}i}{d{t}^2}+(R_1+R_2)\frac{di}{dt}+\frac{i}{C}=-10(15+a)\sin \left(10t\right)$

och sedan med insatta värden på R1, R2, L och C

$\frac{d^{2}i}{d{t}^2}+70\frac{di}{dt}+1000i=-10(15+a)\sin \left(10t\right)$

Mega7853 skrev:

Då ser det ut som att det är tillåtet när ekvationen ser ut på det sättet. Då är det bara att köra på, precis som du har gjort.

Nu när jag tittar lite noggrannare så verkar du har skrivit fel på koefficienten till q(t) (eller i(t) efter derivering). Du har skrivit 2, men det ska väl vara 1/C = 1/0.001 = 1000?

Sen står det (15+a) i uttrycket för u(t), men du har förenklat till 19.

 

Om jag skulle skriva det så skulle det bli

$L\frac{di}{d{t}^{}}+(R_1+R_2)i+\frac{q}{C}=(15+a)\cos \left(10t\right)$

och sedan efter derivering

$L\frac{d^{2}i}{d{t}^2}+(R_1+R_2)\frac{di}{dt}+\frac{i}{C}=-10(15+a)\sin \left(10t\right)$

och sedan med insatta värden på R1, R2, L och C

$\frac{d^{2}i}{d{t}^2}+70\frac{di}{dt}+1000i=-10(15+a)\sin \left(10t\right)$

Precis, jag har ju råkat skriva med. Min fullständiga uträkning ser ut såhär: 

$i\text{'}\text{'}\left(t\right) + 70i\text{'}\left(t\right) + 1000i\left(t\right) = -190\sin \left(10t\right)$.

Haha glömde nämna det! a = första siffran i mina fyra sista siffror i personnumret. Så i mitt fall är det 4.

Provade förresten att köra ekvationen i Matlab och fick följande :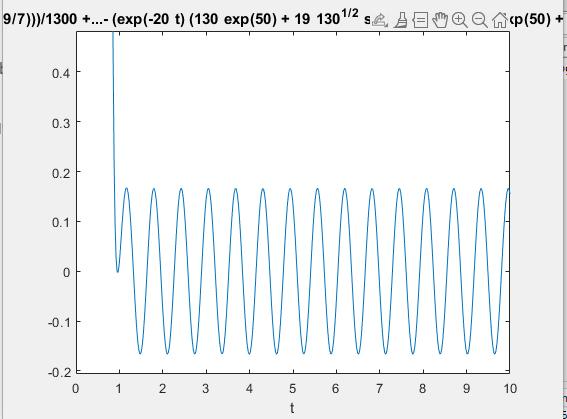

Då har jag använt villkoren i(0) = 12 och i'(0) = 1.

Ganska intressant faktiskt!

Så din fråga gäller egentligen om det är tillåtet att derivera båda sidor av en ekvation? Det är generellt inte tillåtet. 

När skulle det inte vara tillåtet? 

Du kan utföra implicit derivata på varje term utan några som helst problem:

$xy = 1$

$\dfrac{d}{dx}\left(xy\right)=\dfrac{d}{dx}\left(1\right)$

$y + xy' = 0$

Hmm. Jag kommer inte ihåg mycket av detta, bara att vi tog upp ett exempel som inte fungerar. Jag kanske inte förstod problemet här utan drog för långtgående slutsatser av det.

$$\begin{gathered} x=1 \\ \frac{d}{dx}\left(x\right)=\frac{d}{dx}\left(1\right) \\ 1=0 \end{gathered}$$

Uttrycket $x=1$ innehåller ingen implicit funktion $y(x)$ och därmed kan du omöjligt hitta derivatan $y'(x)$. Det är därmed inte ett lämpligt exempel.

Den formella definitionen är nämligen att om du har en implicit ekvation $R(x,y) = 0$ kan du definiera derivatan av den implicita funktionen $y(x)$ som:

$\dfrac{dy}{dx}=- \dfrac{\dfrac{\partial R}{\partial x}}{\dfrac{\partial R}{\partial y}}$

Vi ser genast att eftersom $\dfrac{\partial R}{\partial y}=0$ har vi ett odefinierat uttryck.