ODE problem

Vad är $y(t)$ respektive $p(t)$ för något?

Vad står det i Example 1 om sambandet mellan $y$ och $p$?

LuMa07 skrev:

Vad är $y(t)$ respektive $p(t)$ för något?

Vad står det i Example 1 om sambandet mellan $y$ och $p$?

Såhär står det

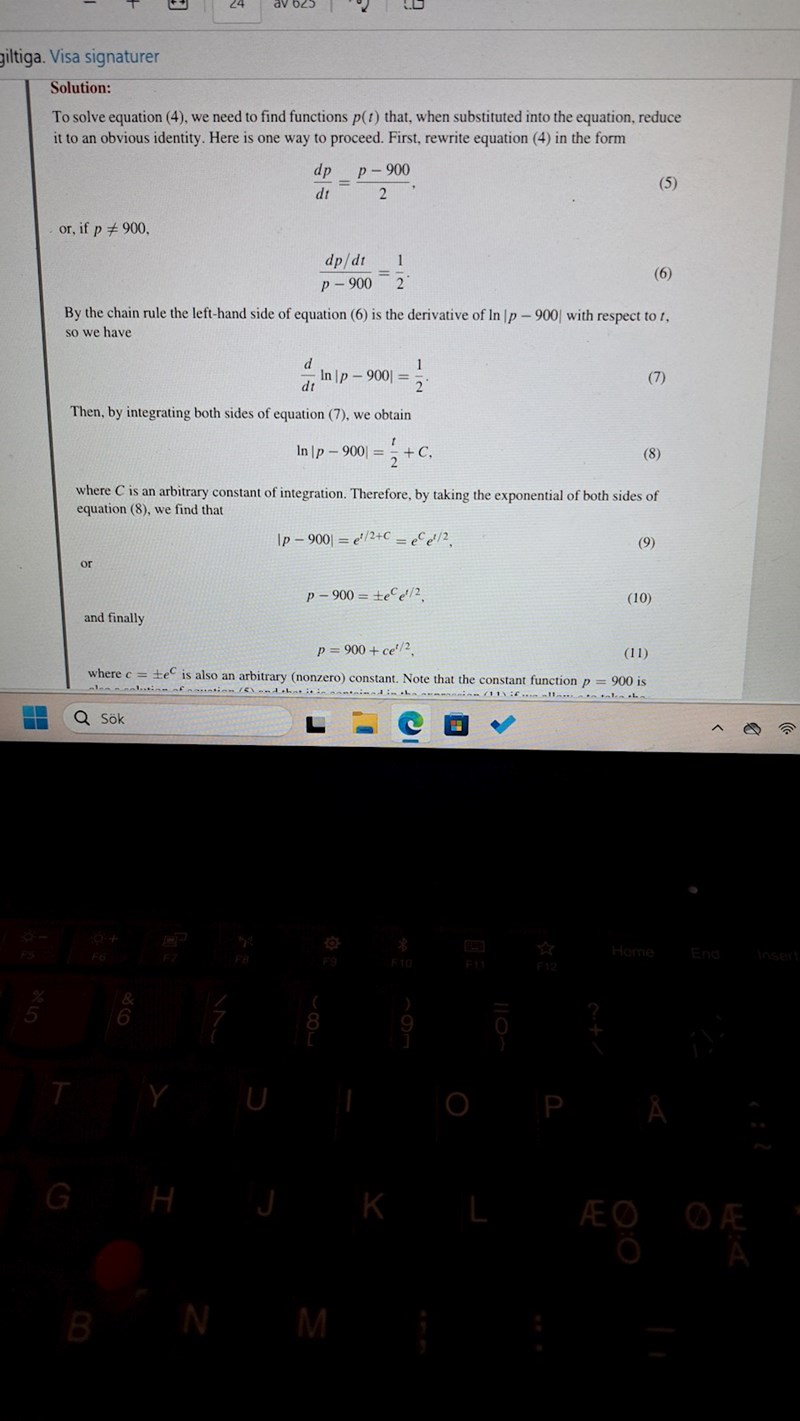
ok, så det verkar vara tryckfel i uppgiftens formulering. Det borde ha varit $\dfrac{dp}{dt}$ i vänsterledet av differentialekvationen.

Fel i din lösning beror på att du brutit ut 1/2 ur 450 utan att ersätta det med 900.

På första raden skriver du $\dfrac{p}{2} - \dfrac{900}{2}$ i HL, vilket är ok.

På andra raden skriver du $\dfrac{1}{2} (p-450)$, vilket är fel. Det borde ha varit $(p-900)$ innanför parentesen.

Nu får jag som dem p(t)=900-50e^1/2t. Men jag förstår inte vad frågan vill i a)

a) De frågar efter tiden då mössen dör ut, d.v.s. $t$-värde då populationen blir 0. Man söker alltså lösningen till ekvationen $900 - 50e^{t/2} = 0$

LuMa07 skrev:

a) De frågar efter tiden då mössen dör ut, d.v.s. $t$-värde då populationen blir 0. Man söker alltså lösningen till ekvationen $900 - 50e^{t/2} = 0$

Aha okej då är jag med. Vad söker i b) och c) ? Jag antar att man ska hitta tiden då populationen också dör ut fast nu har vi annan initialvillkor.

destiny99 skrev:

Aha okej då är jag med. Vad söker i b) och c) ? Jag antar att man ska hitta tiden då populationen också dör ut fast nu har vi annan initialvillkor.

Ja, detta stämmer bra för b)-uppgiften.

c) är en fortsättning av b)-uppgiften. Nu vet du att populationen blir 0 efter ett år, och du söker begynnelsevillkoret som stämmer överens med det. Det är alltså givet att p(1 år) = 0 där uttrycket för p(t) tagits fram i b)-uppgiften, och man vill lösa ut $p_0$.

LuMa07 skrev:

destiny99 skrev:

Aha okej då är jag med. Vad söker i b) och c) ? Jag antar att man ska hitta tiden då populationen också dör ut fast nu har vi annan initialvillkor.

Ja, detta stämmer bra för b)-uppgiften.

c) är en fortsättning av b)-uppgiften. Nu vet du att populationen blir 0 efter ett år, och du söker begynnelsevillkoret som stämmer överens med det. Det är alltså givet att p(1 år) = 0 där uttrycket för p(t) tagits fram i b)-uppgiften, och man vill lösa ut $p_0$.

Jag får dock inte rätt svar i c)

Vad har variabeln t för tidsenheter i den givna modellen (kolla Example 1)?

Val av enheter påverkar om ska sätta t=1, eller t=12, eller t=365

LuMa07 skrev:

Vad har variabeln t för tidsenheter i den givna modellen (kolla Example 1)?

Val av enheter påverkar om ska sätta t=1, eller t=12, eller t=365

Ok jag råkade sätta in t=1 år istället för t=12 mån.