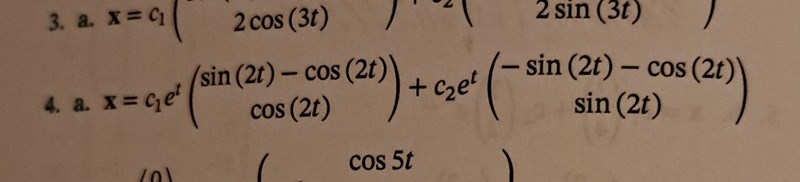Differentialekvationer med komplexa egenvärde

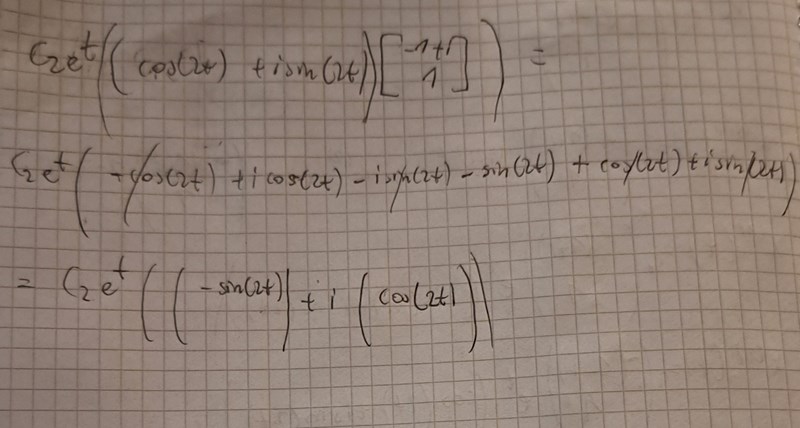

Hej!
Facit får något svar som inte är som jag gjort och jag vet inte hur det är att gruppera den generella lösningen för C1 och C2. Jag fick lambda12 =1+-2i. Jag misstänker att felet ligger på hur jag skalärmultiplicerar komponenterna
är inte korrekt. Det beror på att .
Däremot gäller det att .
Sedan vet jag inte riktigt vad du menar med att "jag skalärmultiplicerar komponenterna". Ingen skalärprodukt ska beräknas här.
LuMa07 skrev:är inte korrekt. Det beror på att .
Däremot gäller det att .
Sedan vet jag inte riktigt vad du menar med att "jag skalärmultiplicerar komponenterna". Ingen skalärprodukt ska beräknas här.
Vad är det som inte är korrekt med x^(2)(t)?
Jag har ju skrivit det i förra inlägget:
Du har skrivit plustecknet framför "i sin(2t)", men det borde ha varit minustecknet!
LuMa07 skrev:Jag har ju skrivit det i förra inlägget:
Du har skrivit plustecknet framför "i sin(2t)", men det borde ha varit minustecknet!
Jag förstår inte varför det skall vara ett minustecken. r=alfa+-Bi och alfa fick vi till 1 vilket är e^alfa och B är -+2
enligt Eulers formel
- Cosinus är en jämn funktion, så .
- Sinus är en udda funktion, så .
Med dessa omskrivningar blir
Lösningen innehåller , så det ska vara där.
Lösningen innehåller , så det ska vara där.
LuMa07 skrev:enligt Eulers formel
- Cosinus är en jämn funktion, så .
- Sinus är en udda funktion, så .
Med dessa omskrivningar blir
Lösningen innehåller , så det ska vara där.
Lösningen innehåller , så det ska vara där.
Jättebra förklaring. Då förstår jag!
Hur ska man förenkla detta nedan? Facits svar nedan är såhär.