Direkt bevis

Gigighena123 skrev:

Hej! 
vart kan jag hitta direkt bevis inom summan av talföljder? Har prov imorgon och i boken finns det inga exempel och min lärare sa att sånt kommer, kan någon hjälpa mig! 
Tack 

De flesta talföljer är inte så enkla att bevisa med direkt bevis men en är

a_n=r*a_{n-1}, r>0, a_0=1

Här behövs ingen induktion etc. 

Vidare, byggt på ovan, så kan du bevisa formeln för 

S_n=1+r+r^2+...+r^n

med ett direkt bevis. För r=2 får du det berömda indiska "ris-problemet"

Det borde väl räcka för att koppla direkt bevis med lite kuriosa inom den matematiska historien.

Finns det inga sidor eller videos på YouTube som kan förklara sånt? Hittar inget i boken och mitt betyg står på det här

Gigighena123 skrev:

Finns det inga sidor eller videos på YouTube som kan förklara sånt? Hittar inget i boken och mitt betyg står på det här

Jag kan ej innehållet på div. matematiksidor och youtube för dåligt.

Om det inte finns i din kursbok (eller utdelade papper), hur kan läraren framhävda att det ingår?

Jag vet inte 🥲 han tog med det på kursprovet och jag fejlade den, så han ska göra en annan sån direkt bevis uppgift för mig att göra för att höja betyget, all bevis på YouTube och i boken är väldigt enkla, det han tog med var väldigt svårt!

Kan du lägga upp det 'svåra' så vi får en känsla för vad det är? Då kanske vi kan ge tips.

En talföljd kan se ut litet hursomhelst, det finns ingen standardformel för dess summa.

Menar du en ARITMETISK följd eller en GEOMETRISK följd  så kan man härleda summaformeln direkt. Se

här är vad som finns i boken men han tog med något med n upphöjt, typ som en summa av talföljder

Det låter som en geometrisk serie. Det betyder att serien har utseendet

a+ak+ak²+ak³+ … + ak^n–1

Talet k kallas kvoten (= 3 i mitt exempel)

Summan fås genom att du tar ”nästa term” minus ”första termen”. Sedan delar du resten med (k–1).

Dvs  S = (akⁿ – a) / (k–1)

Utifrån min bild 2 kan du konstruera ett bevis i det allmänna fallet.

(k får inte vara 1, men i så fall behövs ingen formel.)

Jag förstår inte direkt bevis, kan du ge exempel på det, eller hjälpa mig förstå den

F-n, jag skrev ett långt svar, men det försvann.

Jag tror du ska strunta i ordet ”direkt”. Tänk bevis helt enkelt.

Det finns flera slag av bevis – motsägelsebevis, induktionsbevis mm, men här handlar det om en härledning, som vi kan kalla bevis om vi vill.

Påstående: S_n = a+ak+ak²+…+ak^n–1  = (akⁿ – a)/(k–1)      (för k≠ 1)

Bevis: kS_n = ak+ak²+…+ak^n–1+akⁿ

kS_n – S_n = … … … = akⁿ – a

(k–1)S_n = akⁿ – a

varav påståendet följer.

Jag satsar på ett D, kan du ge mig sånna exempel, boken är väldigt enkla och det min lärare tog med var väldigt svåra 

Sorry, är upptagen ikväll, har inte möjlighet.

Har provet imorn, kan du snälla ge mig ett exempel bara

Jag tycker inte bokens är enkla, långt därifrån. Anser du dem enkla klarar du lätt provet.

2111 tex

Tack så mycket! 
Här är var min lärare svarade nyss när jag skrev till honom om vad jag ska träna på 

hans svar:
Men principen med direkta bevis är likadana oavsett, identifiera en summa, skriv i faktorform eller vad som helst.

2120

Tack så mycket! Detta hjälpte verkligen 🫶🏼🫶🏼🫶🏼

2127

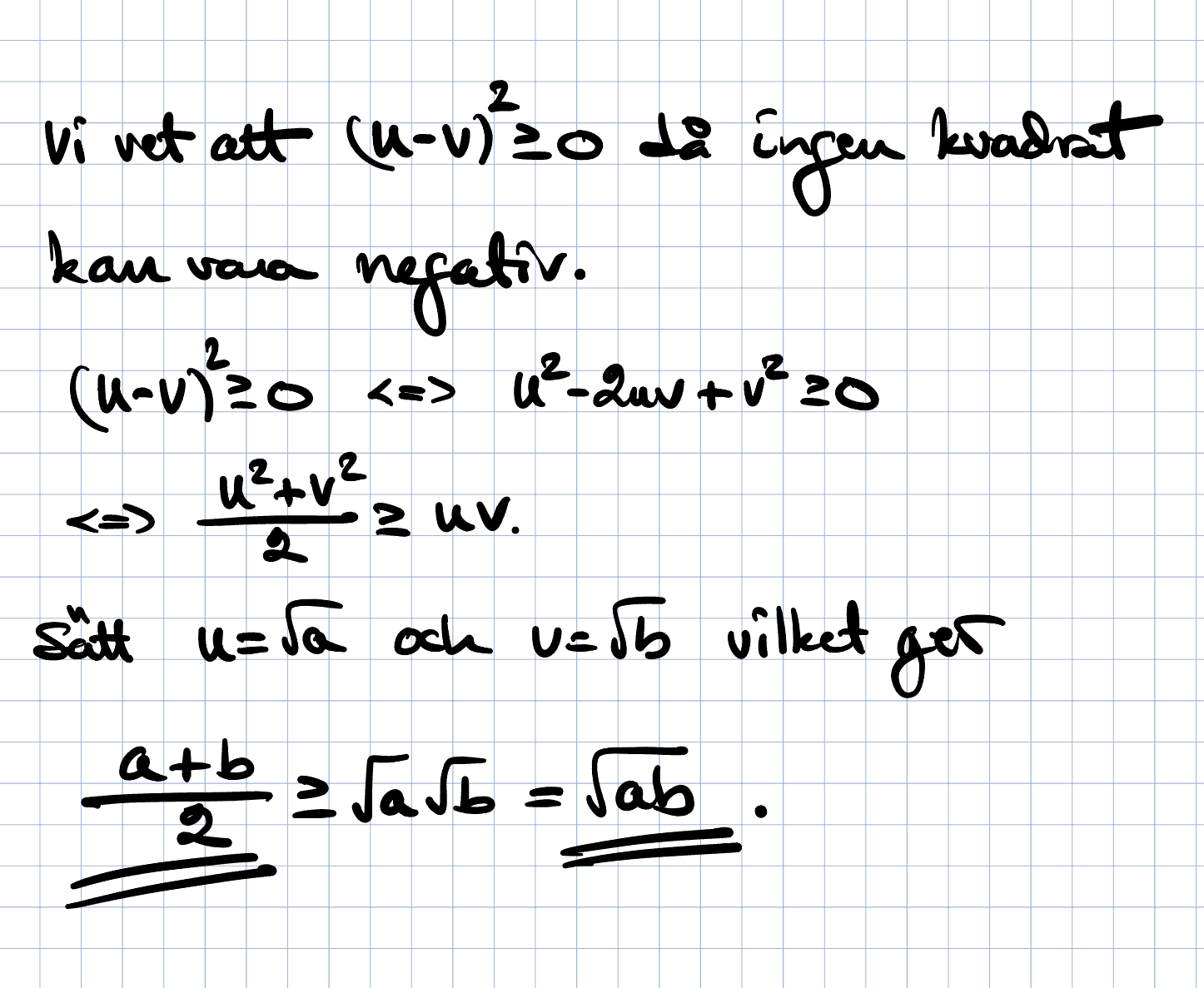
Tack så mycket! 
här är vad min lärare svarade nyss 

2120 är bra. Annars är den klassiska "visa att p⁴-1 inte är ett primtal för p>2" bra, har för mig den var på ett gammalt np

2115

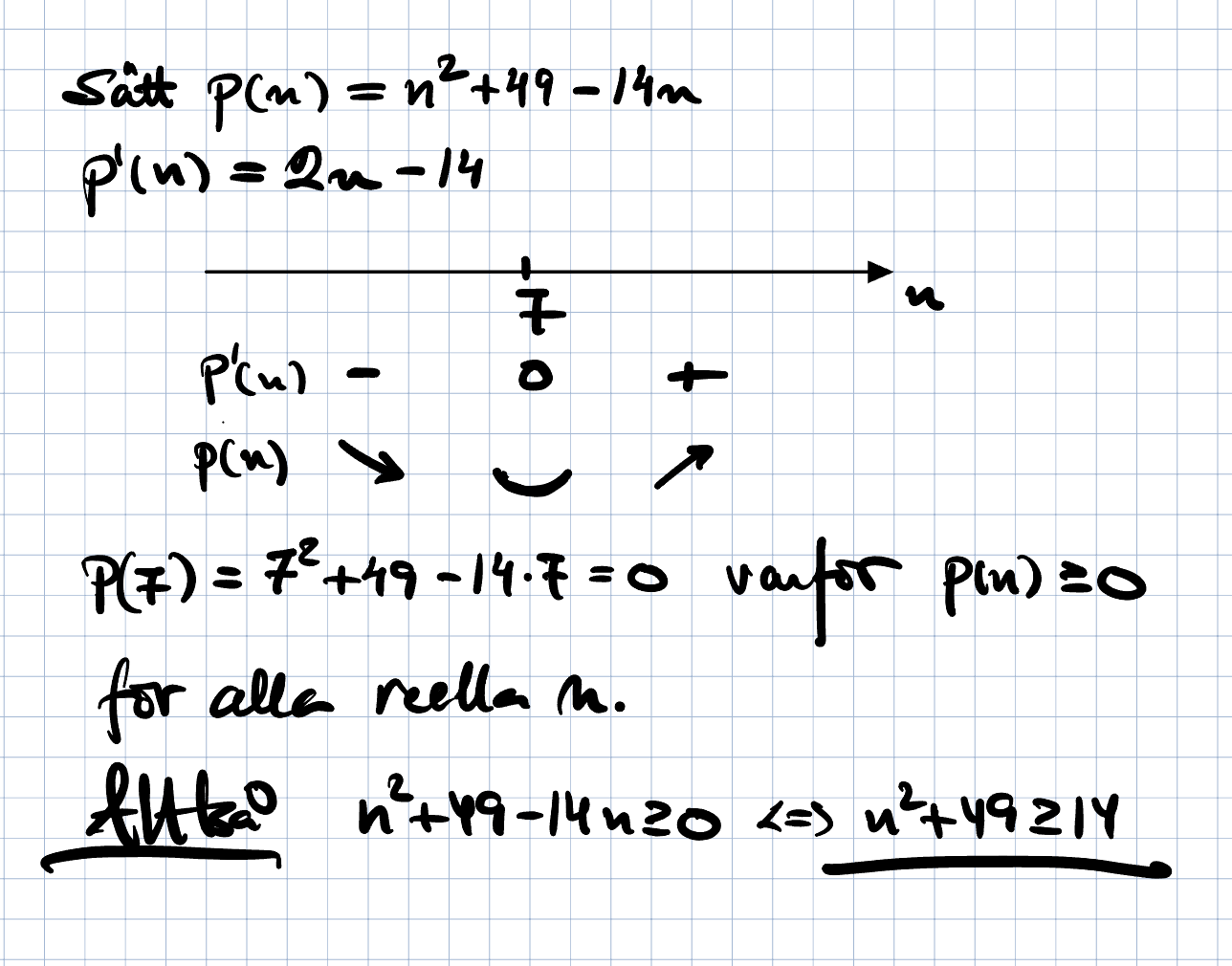
Valet mellan direkt eller indirekt bevisning måste tillhöra den som ska genomföra bevisningen. Den friheten får enligt min åsikt inte inskränkas.