Dubbelintegral

Standardfråga 1a: Har du ritat?

ja jag ritade och får att integrationsområdet hamnar där hyperbeln skär cirkeln i andra kvadranten men jag vet inte hur jag ska gå vidare efter det.

Har du tagit fram skärningspunkterna? Är det helt enkelt de siffrorna som står i uppgiften?

nej jag håller på att försöka ta fram skärningspunkterna, vad jag har sett i liknande exempel så ska man göra ett variabelbyte och få $$\begin{gathered} x=r\cos \theta \\ y=r\sin \theta \end{gathered}$$

och då vi har cirkeln $\sqrt{17}<x^2+y^2<5$ kan vi då skriva om den till $\sqrt{17}<r^2<5$ och dra roten ur och få ${17}^{1/4}<r<\sqrt{5}$

sedan har jag hyperbeln  $1<x^2-y^2<4$ kvar som jag skriver om till $1<r^2\left({\cos }^2\theta -{\sin }^2\theta \right)<4$

men sedan har jag inte kommit längre

Gör ekvationer som du kan lösa istället! Vilka linjer är det som skär varandra i de olika punkterna?

men får man inte då att $r\in \left[{17}^{1/4},\sqrt{5}\right]$ 

När jag ritade fick jag det streckade området som integrationsområde 

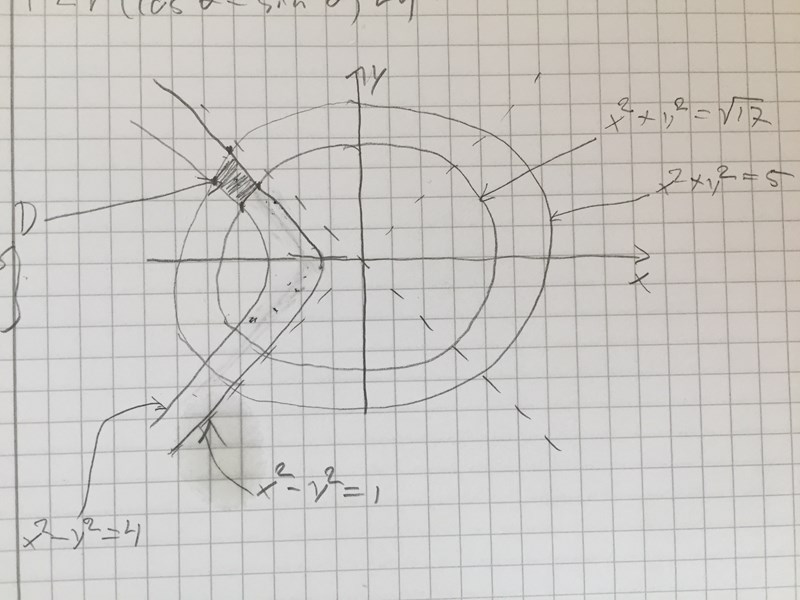
Du har 4 punkter du behöver ta reda på koordinaterna för. Jag tror jag skulle försöka med (x,y) först, men det är möjligt att det blir enklare med polära koordinater. Om man använder polära koordinater så är den "sydöstra" och "nordvästra" begränsningarna enkla, eftersom de är r = k (två olika k), men vad är de båda andra begränsningarna?

För att få fram gränserna till theta gjorde jag:

$1<x^2-y^2<4$ som ifall vi går över till polära koordinater får $1<r^2\left({\cos }^2\theta -{\sin }^2\theta \right)<4$ sedan delar jag samtliga led med $r^2$ och får då $\frac{1}{r^2}<\cos 2\theta <\frac{4}{r2}$ eftersom ${\cos }^2\theta -{\sin }^2\theta =\cos 2\theta$

Då har vi att $\cos 2\theta \in \left[\frac{1}{r^2},\frac{4}{r^2}\right]$ men närmare än så kommer jag tyvärr inte, vi måste ju få ett värde för theta ensamt så att vi sedan har gränsvärden för dubbelintegralen när vi ska börja integrera. Är det någon som har en idê hur man kan göra det? 

Olikheten $\sqrt{17}<><>$ ger dig gränserna för r.

För att få fram de "sydvästra" och "nordöstra" begränsningarna behöver du använda dig av att  den första olikheten ger dig att $1<><>$. Du behöver göra om det till polära koordinater.

Låter förra inlägget vara kvar så att jag kan rapportera buggen. /moderator

Olikheten $\sqrt{17} < x^2+y^2<5$ ger dig gränserna för r.

För att få fram de "sydvästra" och "nordöstra" begränsningarna behöver du använda dig av att  den första olikheten ger dig att $1<x^2-y^2<4$. Du behöver göra om det till polära koordinater.

Hej!

Planpolära koordinater kanske inte är de mest lämpliga här.

Inför istället variablerna $u=x^2-y^2$ och $v=x^2+y^2$ vilket ger integranden

    $\frac{uv}{2\sqrt{v^2-u^2}}$

och integrationsområdet blir en axelparallell rektangel (E) i $uv$-planet. 

    $\displaystyle \iint_E \frac{uv}{2\sqrt{v^2-u^2}}dudv.$

Dubbelintegralen beräknas som två itererade enkelintegraler, där den inre integralen sker med avseende på variabeln $u$; integralen ger ett tal som ligger mellan 2 och 18. 

Albiki skrev:

Hej!

Planpolära koordinater kanske inte är de mest lämpliga här.

Inför istället variablerna $u=x^2-y^2$ och $v=x^2+y^2$ vilket ger integranden

    $\frac{uv}{2\sqrt{v^2-u^2}}$

och integrationsområdet blir en axelparallell rektangel (E) i $uv$-planet. 

    $\displaystyle \iint_E \frac{uv}{2\sqrt{v^2-u^2}}dudv.$

Dubbelintegralen beräknas som två itererade enkelintegraler, där den inre integralen sker med avseende på variabeln $u$; integralen ger ett tal som ligger mellan 2 och 18. 

 Snyggt! Den möjligheten hade jag inte tänkt på.

jag förstår inte riktigt, hur får du $\frac{uv}{2\sqrt{v^2-u^2}}$ ? 

och vad blir då E? 

K.Ivanovitj skrev:

jag förstår inte riktigt, hur får du $\frac{uv}{2\sqrt{v^2-u^2}}$ ? 

och vad blir då E? 

 Du måste vara mer specifik. Exakt vad är det som du inte förstår? Vet du inte hur man gör en variabelsubstitution i en integral?

jag menar om vi har u$=x^2-y^2$ och $v=x^2+y^2$ och den ursprungliga uppgiften var ${\iint }_D\left(x^4-y^4\right)dxdy$

så kan vi ju först helt enkelt sätta ${\iint }_D\left(u\times v\right)dudv$ så lång är jag ju med att vi bara gjort ett variabelbyte. Det jag inte riktigt är med på hur vi går från det till att sätta $\frac{uv}{2\sqrt{v^2-u^2}}$, integranden av u*v blir väl $\frac{u^2{v}^2}{4}$ ?

och sedan får vi det nya integrationsområdet E blir det då E=$\left\{1<u<4, \sqrt{17}<v<5, x<0, y>0\right\}$

E blir jätteenkelt: $1<><4, \=""><><>$

Använd konjugatregeln baklänges på $x^4-y^4$ innan du gör om funktionen till u och v. Använd konjugatregeln framlänges efteråt.

Vad blir dudv uttryckt i dxdy?

EDIT: tänkte fel förut

om jag använder konjugatregeln baklänges på $x^4-y^4$ får vi väl $x^4-y^4=\left(x^2+y^2\right)\left(x^2-y^2\right)$  och får då att $u=x^2+y^2$ och $v=x^2-y^2$ men vad menar du att man ska göra sen?

sedan blir väl du=$2x$ och dv=2y

blir E då $\left\{1<v<4, \sqrt{17}<u<5, \frac{1}{2}u<0, \frac{1}{2}v>0\right\}$

Du har fel uttryck för du och dv. Både du och dv beror både på x och y och därmed på dx och dy.

okej så får vi då att du=$2x+2y$ och dv=2x-2y?

Vad blir då $du \cdot dv$?

då får vi $\left(2x+2y\right)(2x-2y)=4x^2-4y^2$ 

Jag får ta ett steg tillbaka och erkänna att jag verkar ha lurat dig på villovägar. Det verkar bättre att försöka göra tvärtom och uttrycka $dxdy$ som $dudv$ istället. Vad blir det?

Till T.S. Du måste lära dig om funktionaldeterminanter vid variabelsubstitution då man beräknar flerdimensionella integraler.

Uppgift: Bestäm funktionaldeterminanten (ä.k. Jacobianen) $\frac{dxdy}{dudv}$.

för $\frac{dxdy}{dudv}$ gäller väl $\frac{dxdy}{dudv}=\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|$ och om vi nu har $u=x^2+y^2 och v=x^2-y^2$ kan man då sätta $\frac{dudv}{dxdy}=\left|\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}\end{array}\right|=\left|\begin{array}{cc}2x& 2y\\ 2x& -2y\end{array}\right|=-8\left(xy\right)$

K.Ivanovitj skrev:

för $\frac{dxdy}{dudv}$ gäller väl $\frac{dxdy}{dudv}=\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|$ och om vi nu har $u=x^2+y^2 och v=x^2-y^2$ kan man då sätta $\frac{dudv}{dxdy}=\left|\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}\end{array}\right|=\left|\begin{array}{cc}2x& 2y\\ 2x& -2y\end{array}\right|=-8\left(xy\right)$

 Varför beräknar du $\frac{dudv}{dxdy}$ när det är $\frac{dxdy}{dudv}$ som du behöver?

jag förstår inte hur ska vi ta derivatan av x med avseende på u, har vi att $u=x^2+y^2$ och kan då flytta över u till $x^2=y^2-u\Rightarrow x=y-\sqrt{u}$ och ska vi sedan ta derivatan av detta uttryck med avseende på u? i så fall får vi att $\frac{\partial x}{\partial u}=\frac{1}{2\sqrt{u}}$

$x^2=y^2-u=>x=y-\sqrt{u} FEL! Glöm inte bort att \sqrt{a+b}=/=\sqrt{a}+\sqrt{b.}$

gjorde fel,

$\frac{\partial x}{\partial u}=$   x=$\pm \sqrt{y^2-u}$ ska det vara 

Räknar jag ut $\frac{dxdy}{dudv}$ får jag tillslut att $\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|=\left|\begin{array}{cc}\pm \sqrt{u-y^2}& \pm \sqrt{v+y^2}\\ \pm \sqrt{u-x^2}& \pm \sqrt{x^2-v}\end{array}\right|$ men sedan känner jag mig lite vilsen i hur man ska gå vidare.  Hur får vi att den inre integralen med avseende på u ger ett tal som ligger mellan 2 och 18?

Eftersom integrationsområdet kräver att $x<>$ och $y>0$ så gäller det att

    $x=-\sqrt{\frac{u+v}{2}}$ och $y=\sqrt{\frac{v-u}{2}}$.

För att detta ska fungera måste det gälla att $v\geq u\geq 0$; är dessa villkor uppfyllda i detta problem? 

om vi använder att du satte $u=x^2-y^2$ och v=$x^2+y^2$ från början så har vi att $v\ge u\ge 0$ eftersom varken x eller y får vara noll så blir båda termer positiva.

Att $u$ och $v$ är positiva är självklart; den intressanta frågan är om $v\geq u$.

ja då blir väl $v\ge u$ då vi har restriktionerna x<0 och y>0

K.Ivanovitj skrev:

ja då blir väl $v\ge u$ då vi har restriktionerna x<0 och y>0

 Nej! Det följer inte att $v\geq u$ bara för att $x<>$ och $y>0$. Hur tänkte du där?

jag satte ett godtyckligt negativ tal som x och positivt som y då får jag för u ett positivt tal minus ett annat positivt tal och för v ett positivt tal plus ett annat positivt tal och därmed borde v vara större än u

K.Ivanovitj skrev:

jag satte ett godtyckligt negativ tal som x och positivt som y då får jag för u ett positivt tal minus ett annat positivt tal och för v ett positivt tal plus ett annat positivt tal och därmed borde v vara större än u

 Eftersom $y^2$ aldrig är negativt följer det att $x^2+y^2\geq x^2-y^2$. 

Beräkna nu den relevanta funktionaldeterminanten $\frac{dxdy}{dudv}$.

jag får $J=\frac{d\left(x,y\right)}{d\left(u,v\right)}=\left|\begin{array}{cc}-\frac{1}{2\sqrt{2}\sqrt{u+v}}& -\frac{1}{2\sqrt{2}\sqrt{u+v}}\\ -\frac{1}{2\sqrt{2}\sqrt{v-u}}& \frac{1}{2\sqrt{2}\sqrt{v-u}}\end{array}\right|$

med x=$-\sqrt{\frac{u+v}{2}}$ och y=$\sqrt{\frac{v-u}{2}}$

Bra, kom också ihåg att den lokala areaförstoringen under avbildningen ges av absolutbeloppet av funktionaldeterminanten.

Du var också god väg i ett tidigare inlägg. Ett alternativt sätt att nå resultat är att utnyttja att inversens funktionaldeterminant i en punkt är samma tal som det inverterade värdet av funktionens funktionaldeterminant, dvs

$\frac{\partial(x,y)}{\partial(u,v)}=\frac{1}{\frac{\partial(u,v)}{\partial(x,y)}}=\frac{1}{\begin{vmatrix}2x&2y\\2x&-2y \end{vmatrix}}=\frac{1}{-8xy}$ vilket du nästan kom fram till ovan.

Nu noterar vi att

$\sqrt{u^2-v^2}=2|xy|$ varför absolutbeloppet av $|J|$ alltså kan skrivas $\frac{1}{4\sqrt{u^2-v^2}}$

Edit: Nu räknade jag med $u=x^2+y^2$ och $v=x^2-y^2$ istället för vice versa, men det är bara att byta plats på u och v.

okej vad bra då kom funktionaldeterminanten fram :) när vi nu har fått fram den och vet att $u=x^2-y^2$ och $v=x^2-y^2$ vad blir då nästa steg? vi hade ju sedan tidigare att integrationsområdet var E=$\left\{1<u<4, \sqrt{17}<v<5\right\}$ sedan hade vi även restriktionen x<0 och y>0 när vi nu har funktionaldeterminanten $\frac{1}{4\sqrt{u^2-v^2}}$ hur kan vi då skriva E? 

Med $u=x^2-y^2$ och $v=x^2+y^2$ är det viktigt att du väljer absolutbeloppet av determinanten som $\frac{1}{4\sqrt{v^2-u^2}}$, eftersom $v>u$ i definitionen av ditt område.

Vet inte om ni konstaterat det ännu, men $x^4-y^4=(x^2+y^2)(x^2-y^2)=vu$

Integralen ges nu alltså av

$\displaystyle \iint_E uv|J|\,dudv$

att uv blir $x^4-y^4$ vilket är vad vi har från början i uppgiften är jag med på, dock inte hur vi ska integrera ${\iint }_{E}uv\left|J\right|dudv$

inom E har vi ju begränsningarna 1<u<4 och $\sqrt{17}<v<5$ ska vi då sätta ${\int }_1^4{\int }_{\sqrt{17}}^{5}uv\left|J\right|dudv$

ska vi sätta I=${\iint }_E\frac{ub}{4\sqrt{u^2-v^2}}dudv$ och sedan ha integrationsgränserna $I={\int }_1^4{\int }_{\sqrt{17}}^5\frac{uv}{4\sqrt{u^2-v^2}}dudv$

Ja. Men notera att du nu använde

 --------------------------------------------------------------------------------------------------------------

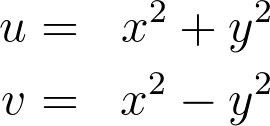
Som avslutning och överkurs kan det också vara intressant att studera problemet i polära koordinater.

Du kom (nästan) fram till att

$\arccos(\frac{1}{r^2})<><>$

Vinkeln ska peka på den andra kvadranten. Eftersom integranden antar exakt samma värden på båda sidor om y-axeln och integrationsområdet  är spegelsymmetriskt kring y kan vi lika gärna beräkna integralen för den första kvadranten (så slipper vi justera vinkeln).

Vi kommer ihåg att för $x>0$ gäller

$\arccos(x)=\arcsin(\sqrt{1-x^2})$

Alltså blir gränserna för $\theta$

$\displaystyle \arcsin(\sqrt{1-\frac{16}{r^4}}) <2\theta><>$

Slutligen är $x^4-y^4$=$(x^2-y^2)(x^2+y^2)=r^4\cos(2\theta)$.

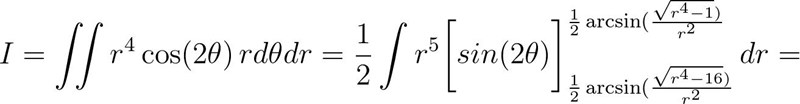
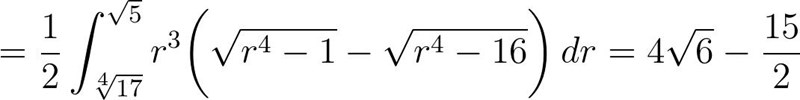
Edit: Nu har jag förhoppningsvis lagat hela inlägget med bilder istället.

okej, för att ha kvar $u=x^2-y^2$ och $y=x^2+y^2$ kan jag väl bara byta ordningen på integralerna så vi får ${\int }_{\sqrt{17}}^5{\int }_1^4\frac{uv}{4\sqrt{u^2-v^2}}dudv$

Om man sedan tittar på hur man kan lösa uppgiften med polära koordinater så är jag inte helt med på $arc\cos \left(x\right)=arc\sin \left(\sqrt{1-x^2}\right)$ 

sedan sätter vi in $x=\left(\frac{4}{r^2}\right)$ i $\sqrt{1-x^2}$ och får då $arc\sin \left(\sqrt{1-\frac{16}{r^4}}\right)$ det är jag med på.

K.Ivanovitj skrev:

okej, för att ha kvar $u=x^2-y^2$ och $y=x^2+y^2$ kan jag väl bara byta ordningen på integralerna så vi får ${\int }_{\sqrt{17}}^5{\int }_1^4\frac{uv}{4\sqrt{u^2-v^2}}dudv$

Det som spelar roll är alltså det som står under rottecknet. Du vill inte att det ska bli ett negativt tal vilket det blir om $u^2-v^2<>$, vilket det är då $u=x^2-y^2$.

Själva integralen blir väldigt enkel om du ser att $\displaystyle \frac{\mathrm{d} }{\mathrm{d} v}\left(\sqrt{v^2-u^2}\right)=\frac{1}{2\sqrt{v^2-u^2}}\cdot 2v=\frac{v}{\sqrt{v^2-u^2}}$

I nästa integrationssteg kan du återigen tillämpa ungefär samma trick.

okej den andra får jag $\frac{d}{du}\left(\sqrt{v^2-u^2}\right)=-\frac{u}{\sqrt{v^2-u^2}}$

men om man ska lösa uppgiften med polära koordinater istället är jag med fram till att vi får gränsvärdena $\frac{1}{2}arc\sin \left(\sqrt{\frac{r^4-1}{r^2}}\right)$ och $\frac{1}{2}arc\sin \left(\frac{r^4-16}{r^2}\right)$  hur får vi fram dom? och varför har vi 1/2 framför integralen?

Guggle skrev:

Ja. Men notera att du nu använde

 --------------------------------------------------------------------------------------------------------------

Som avslutning och överkurs kan det också vara intressant att studera problemet i polära koordinater.

Du kom (nästan) fram till att

$\arccos(\frac{1}{r^2})<><>$

Vinkeln ska peka på den andra kvadranten. Eftersom integranden antar exakt samma värden på båda sidor om y-axeln och integrationsområdet  är spegelsymmetriskt kring y kan vi lika gärna beräkna integralen för den första kvadranten (så slipper vi justera vinkeln).

Vi kommer ihåg att för $x>0$ gäller

$\arccos(x)=\arcsin(\sqrt{1-x^2})$

Alltså blir gränserna för $\theta$

$\displaystyle \arcsin(\sqrt{1-\frac{16}{r^4}}) <2\theta><>$

Slutligen är $x^4-y^4$=$(x^2-y^2)(x^2+y^2)=r^4\cos(2\theta)$.

Edit: Nu har jag förhoppningsvis lagat hela inlägget med bilder istället.

 jag förstår hur man får fram $arc\sin \left(\sqrt{1-\frac{16}{r^4}}\right)=arc\sin \left(\sqrt{\frac{r^4-16}{r^4}}\right)=arc\sin \frac{\sqrt{r^4-16}}{r^2}$ men inte hur vi får $\frac{1}{2}arc\sin \frac{\sqrt{r^4-16}}{r^2}$

sedan är jag med på integralen $\int r^5\left[\sin \left(2\theta \right)\right]$ men inte hur vi får $\frac{1}{2}\int r^5\left[\sin \left(2\theta \right)\right]$ så det är något med divisionen 1/2 jag har missat.

kommer 1/2 både i $\frac{1}{2}\int r^5$ och ${\left[\sin \left(2\theta \right)\right]}_{\frac{1}{2}arc\sin \frac{\sqrt{r^4-16}}{r^2}}^{\frac{1}{2}arc\sin \frac{\sqrt{r^4-1}}{r^2}}$dr av att vi har haft gränserna för $\theta$ uttryckt för $2\theta$ ? eftersom vi satte integrationsgränserna $arc\sin \left(\sqrt{1-\frac{16}{r^4}}\right)<2\theta <arc\sin \left(\sqrt{1-\frac{1}{r^4}}\right)$ vilket då ger oss gränserna $\frac{1}{2}arc\sin \left(\sqrt{1-\frac{16}{r^4}}\right)<\theta <\frac{1}{2}arc\sin \left(\sqrt{1-\frac{1}{r^4}}\right)$

och för integralen har vi $\frac{1}{2}\int r^5\left[\sin \left(2\theta \right)\right]$ dvs 2$\theta$

Vi har kommit fram till att

$\frac{1}{r^2}<><>$

Detta uttryck ska gälla för vissa $\theta$ i den andra kvadranten. Men det blir enklast att studera vad villkoret betyder i den första kvadranten (så slipper vi hantera $2\pi-\arccos(..)$-uttryck). Detta kan vi välja att göra eftersom det råder symmetri  (för såväl integrand som integrationsområde).

I den första kvadranten ser $cos(2\theta)$ ut så här. 

Vi inser alltså att $2\theta$ måste satisfiera

$\arccos(\frac{4}{r^2})<><>$

Nu ersätter vi $\arccos(x)=\arcsin(\sqrt{1-x^2})$ samt delar båda sidor med 2.

$\displaystyle \frac{1}{2}\arcsin(\sqrt{1-(\frac{4}{r^2})^2})<><>$

Därav $\frac{1}{2}$ i integrationsgränserna.

Den primitiva funktionen till $\cos(2\theta)$

$\int \cos(2\theta)\,d\theta=\frac{1}{2}\sin(2\theta)$

Därav en faktor $\frac{1}{2}$ framför integralen när vi integrerat i $\theta$.

okej då förstår jag den delen nu, men hur kommer det sig att vi får $r^3$ framför $\left(\sqrt{r^4-1}-\sqrt{r^4-16}\right)$

K.Ivanovitj skrev:

okej då förstår jag den delen nu, men hur kommer det sig att vi får $r^3$ framför $\left(\sqrt{r^4-1}-\sqrt{r^4-16}\right)$

 Är du med på att integralen du vill beräkna är

$\displaystyle I=\iint r^4\cos(2\theta)\,rd\theta dr$?

Du kan bryta ut en $\frac{1}{r^2}$ ur rotuttrycken som kommer från integrationsgränserna i $\theta$-led.

Sedan gäller $\frac{r^5}{r^2}=r^3$.

Ett allmänt tips är att du själv försöker beräkna integralen och använder mina mellansteg som de kontrollpunkter och tips de är avsedda för. Just nu verkar du snarare försöka förstå varje mellansteg istället för att räkna själv.

ja det är jag med på att vi ska beräkna $I={\iint }_D{r}^4\cos \left(2\theta \right)rd\theta dr$

sedan har vi  $r^5$$\frac{1}{2}\int r^5\left[\sin \left(2\theta \right)\right]$ eftersom vi multiplicerar in r från $rd\theta dr$ med $r^4$

och vi har gränsvärdena $r\in \left[\sqrt[4]{17},\sqrt{5}\right]$ och $\varnothing \in \left[\frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-16}}{r^2}\right), \frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-1}}{r^2}\right)\right]$

och ska då beräkna $I={\int }_{r=\sqrt[4]{17}}^{\sqrt{5}}{\int }_{\theta =\frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-16}}{r^2}\right)}^{\frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-1}}{r^2}\right)}{r}^4\cos \left(2\theta \right)rd\theta dr$

börjar vi då med att integrera i theta led sätter vi ${\left[\sin \left(2\theta \right)\right]}_{\frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-16}}{r^2}\right)}^{\frac{1}{2}arc\sin \left(\frac{\sqrt{r^4-1}}{r^2}\right)}dr$ 

sedan integrerar vi i r-led:$1=\frac{1}{2}{\int }_{\sqrt[4]{17}}^{\sqrt{5}}{r}^3\left(\sqrt{r^4-1}-\sqrt{r^4-16}\right)dr =\frac{1}{2}\left(8\sqrt{6}-15\right)$

jag tror att jag är med på det mesta nu, men jag är dock inte helt med på övergången från $\frac{1}{r^2}<\cos \left(2\theta \right)<\frac{4}{r^2}$ till $arc\cos \left(\frac{4}{r^2}\right)<2\theta <arc\cos \left(\frac{1}{r^2}\right)$ varför ersätter vi cos med arccos ?

K.Ivanovitj skrev:

jag tror att jag är med på det mesta nu, men jag är dock inte helt med på övergången från $\frac{1}{r^2}<\cos \left(2\theta \right)<\frac{4}{r^2}$ till $arc\cos \left(\frac{4}{r^2}\right)<2\theta <arc\cos \left(\frac{1}{r^2}\right)$ varför ersätter vi cos med arccos ?

 Eftersom du vill integrera med avseende på $\theta$, så vill du ju hitta nedre och övre gräns för  den variabeln.

ja det är jag med på, men jag har lite problem med själva motiveringen till arccos, underlättar det alltså att gå över till arccos istället för att hålla kvar cosinus när vi ska hitta gränserna för theta?

Eftersom theta är en vinkel - ja.