dubbelintegral mha stokes sats för triangel

Hej jag har följande uppgift:

curl F är given = (-11,7,-1) och även normalen n = 1/7(-6,-2,3). Därför blir dubbelintegralen för triangeln ABC

$\iint 7 d x d y$

Där triangeln ligger i detta plan:

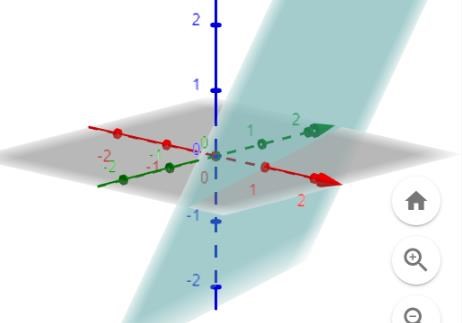
där ekv lyder z = -2+2x+(2y)/3

men eftersom z går från -2 till 0 bör -2<= -2+2x+(2y)/3 <=0

vilket ger: -3x<=y<=3-3x

därför tycker jag att gränserna på integralen bör vara

$\int_{0}^{1} (\int_{- 3 x}^{3 - 3 x} 7 d y) d x$ = 21 men det är fel. Kan nångon förklara varför. :)

Du har läst fel. Integralen är $\iint 7 d S$ inte $\iint 7 d x d y$

jo men jag har för mig att ds är samma sak som dx dy hur som hälst så vet jag inte hur jag skulle göra om det är ds. Och det är ju en dubbel integral och inte en trippel

dS är ett areaelement som definieras som $∥ r_{s}' (s, t) \times r_{t}' (s, t) ∥ d s d t$ . Om r(s,t) är en parametrisering av ytan. I detta fall har du dock en integral av formen $\iint 1 d S$ dvs arean av ytan. Istället för att räkna ut integralen kan du därför beräkna arean av triangeln.

Svara

Visa senaste svar