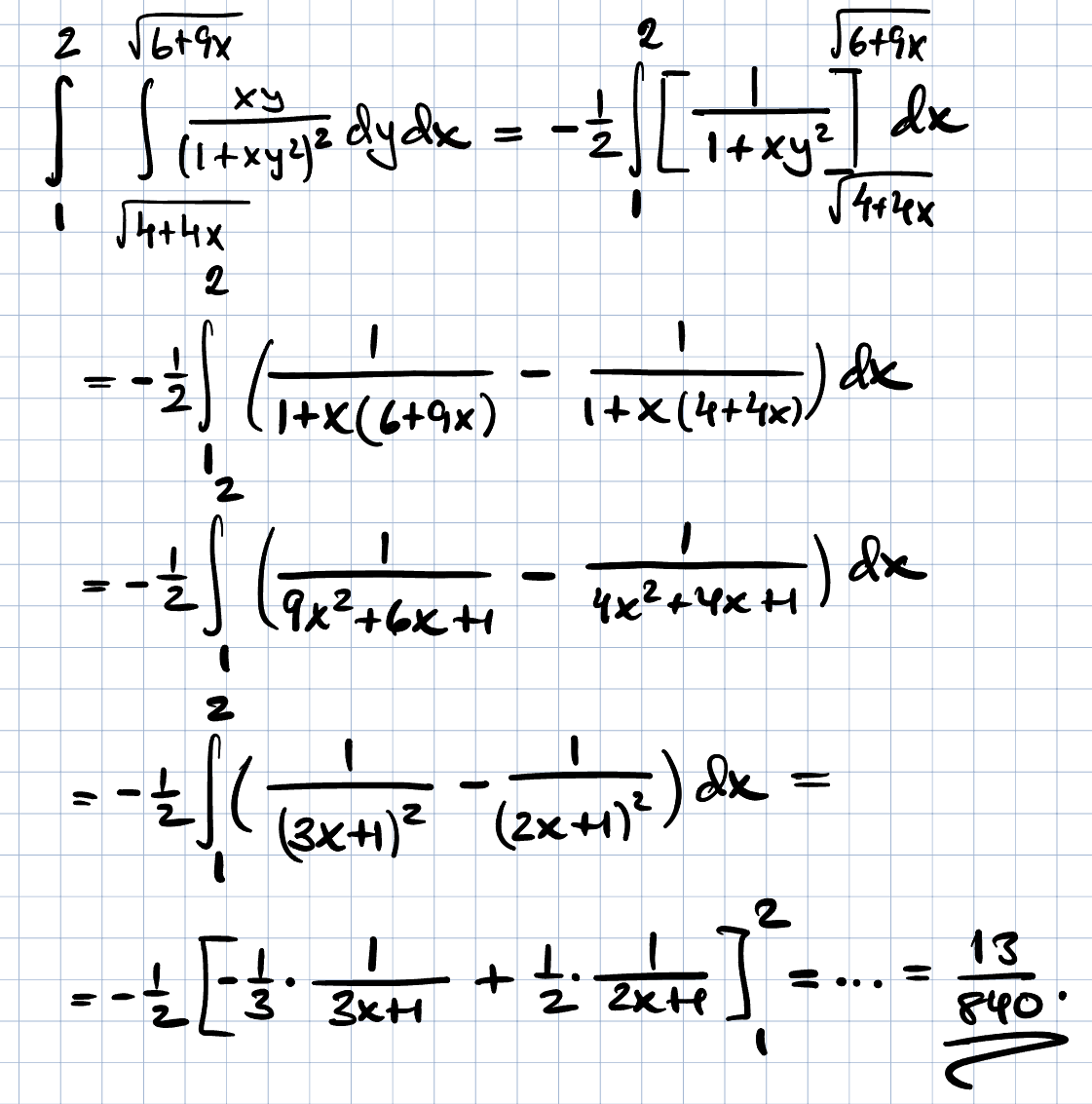
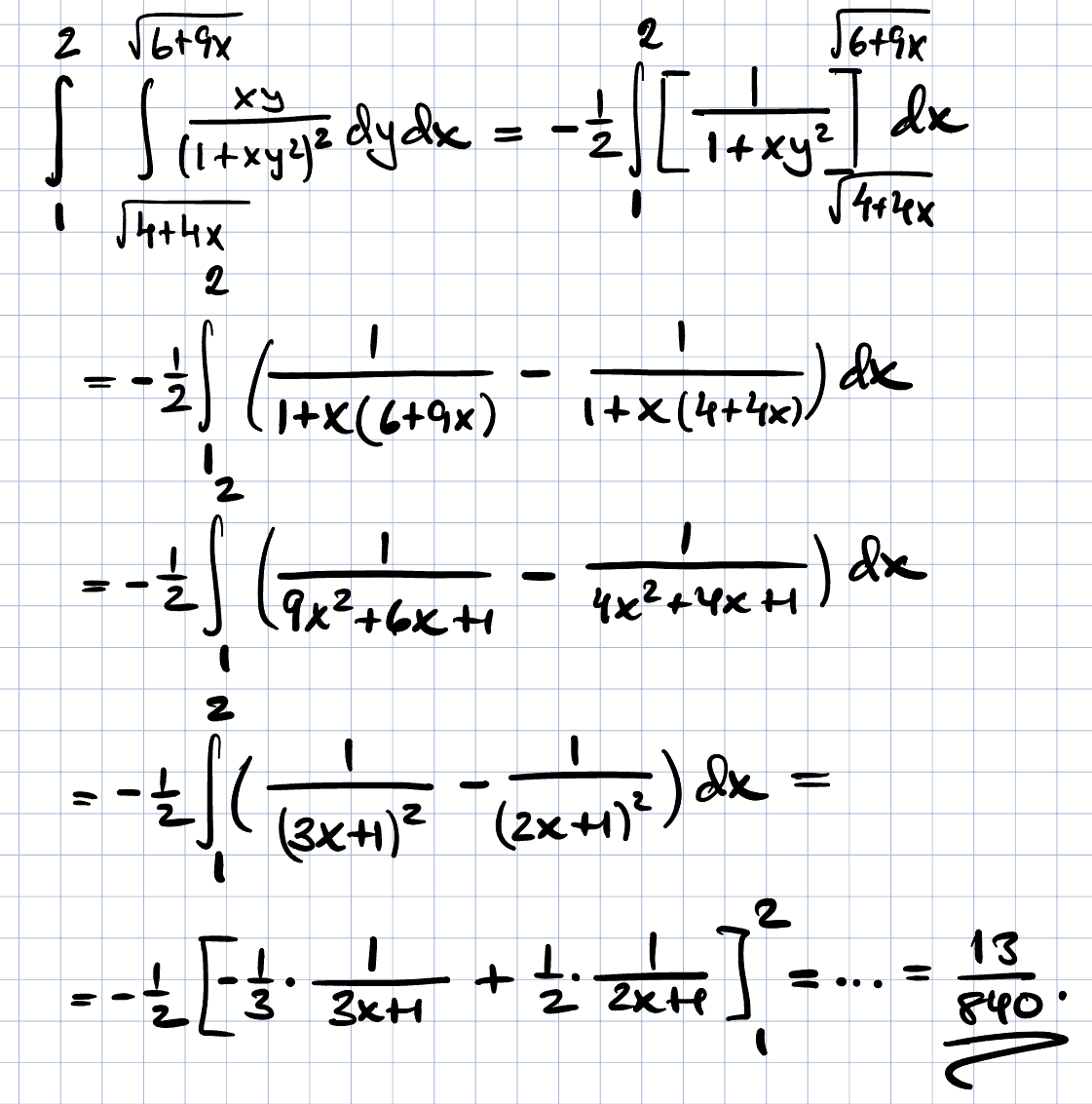
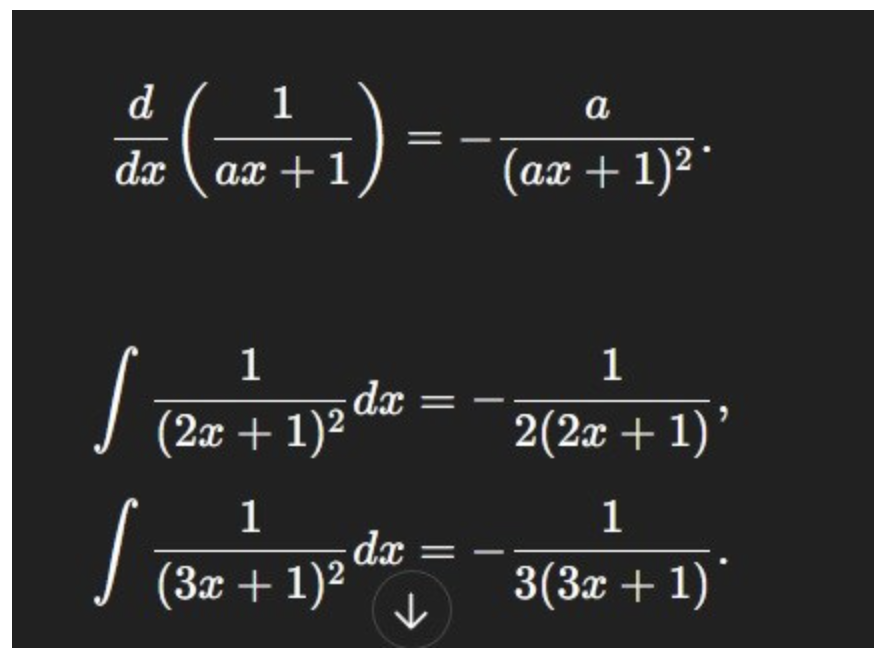Dubbelintegral uppgift

Kolla denna uppgiften är konstig eller så är det bara jag, den känns så svårberäknad med alla bråktal. Jag prövade dubbelvariabelsubstitution (med u,v och inkluderade jakobideterminanten)... svaret krävde miniräknare och ändå blev det fel. Jag frågade Chatgpt också och den fick fram att detta skulle användas. Måste jag kunna denna?
Aja jag använde mig av sedan av dv=2xydy (för kom nyss ihåg att man kunde substituera och nu tror jag jag vet varför det alltid är 2xy, det är på grund av derivatan av 1+xy2 blir just 2xy). Aja, och sen så var bråk beräkningen också inte så himla rolig... asså... jag venne... detta är bara en uppgift.
En annan och sista fråga är varför kan jag inte, efter jag substituerat med v = 1+xy2 och bestämt dess gränser... Varför måste jag bara substituera in för vad y är. Varför kan jag inte sätta in vad x var definierad för också eller blir det konstigt vid integraler... liksom vi vet ju vad x kan vara som minst och mest men Chatgpt säger att vi bör ha x i olikheterna... Varför?

Trinity2 skrev:
asså de är elaka :(
Också hur visste du att det var integralen? Är det något jag missar eller är det bara något jag ska komma ihåg?
Vilket steg menar du?
Trinity2 skrev:Vilket steg menar du?
Första ekvationen längst upp
Menar du dessa?
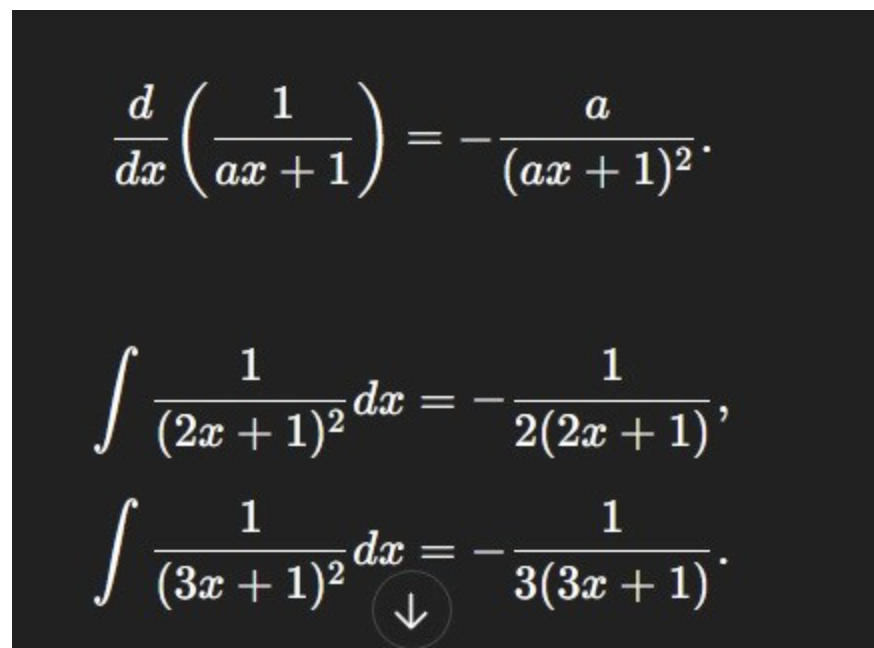
Trinity2 skrev:Menar du dessa?
Visa spoiler
Skriv ditt dolda innehåll här
Ja, är det rätt, hur är det rätt och är det en sådan sak man bara ska komma ihåg? Är detta en sådan klassisk derivata?
Ja, det är en
vanlig D(xN) = N*x(N-1)
på samma sätt som derivatan av x7 är 7*x6
gäller
vanlig D(x-1) = -1*x(-2)
och så får man kompensera med 1/3 där det står 3.
Bubo skrev:Ja, det är en
vanlig D(xN) = N*x(N-1)
på samma sätt som derivatan av x7 är 7*x6
gäller
vanlig D(x-1) = -1*x(-2)
och så får man kompensera med 1/3 där det står 3.
ahh omg, inre derivata gånger yttre derivata (kedjeregeln) yes okej nu hänger jag med. Tack så mycket!