Dubbelvinkel formler

God morgon!

Jag har lite trubble med halvavinklar formlerna (som ingår i en repetition till en ny kurs som vi ska börja med en ärad Nemesis):

Frågan lyder:

Hur många lösningar har den trigonometriska ekvationen i det angivna intervallet?

$cos(x)=\frac14$ i intervallet $-2\pi,3\pi$

Jag har använt formeln för dubbel vinkel:

$cos^2(x)=\frac{1+cos(2x)}2$ med $cos(2x)=\frac12$ dvs $\frac\pi3$ såklart.

$cos^2(x)=\frac{1+0.5}2$

$cos(x)=\pm\sqrt{\frac34}$

Som ger $\frac\pi6,\frac{5\pi}6,\frac{7\pi}6,\frac{11\pi}6$ .

Så jag räknade att på intervalet $\left[-2\pi;3\pi\right]$ kommer jag att få 4 lösningar från $\left[-2\pi;0\right]$ , 4 till mellan $\left[0;2\pi\right]$ och ytterligare två mellan $\left[2\pi;3\pi\right]$ .

Rätt svar är bara 5 lösningar.

Vad har jag tänkt fel?

Om du ritar upp enhetscirkeln ser du att ekvationen har två lösningar i intervallet $[0,2 \pi]$ d v s på ett varv. Intervallet i uppgiften är 2½ varv så det blir 5 lösningar.

Varför krångla till det? (Du har fått med en massa vinklar där cos(x) = -1/4 också.)

Smaragdalena skrev:
Om du ritar upp enhetscirkeln ser du att ekvationen har två lösningar i intervallet $[0,2 \pi]$ d v s på ett varv. Intervallet i uppgiften är 2½ varv så det blir 5 lösningar.

Vänta, nu det är säkert kaffebrist men....

Varför inte 4 lösningar på ett varv?

Varför krångla till det? (Du har fått med en massa vinklar där cos(x) = -1/4 också.)

Har jag det? Tillhör $-\frac{1}4$ till de standard vinklarna?

(Edit: jag ersatt klassiska med standard, pi/3 pi/6 och pi/4)

Du behöver inte få fram ett värde för x som är lösning till ekvationen. Det räcker med att rita lite.

Börja på -2π och snurra 2.5 varv moturs. Lösningar passeras 5 gånger.

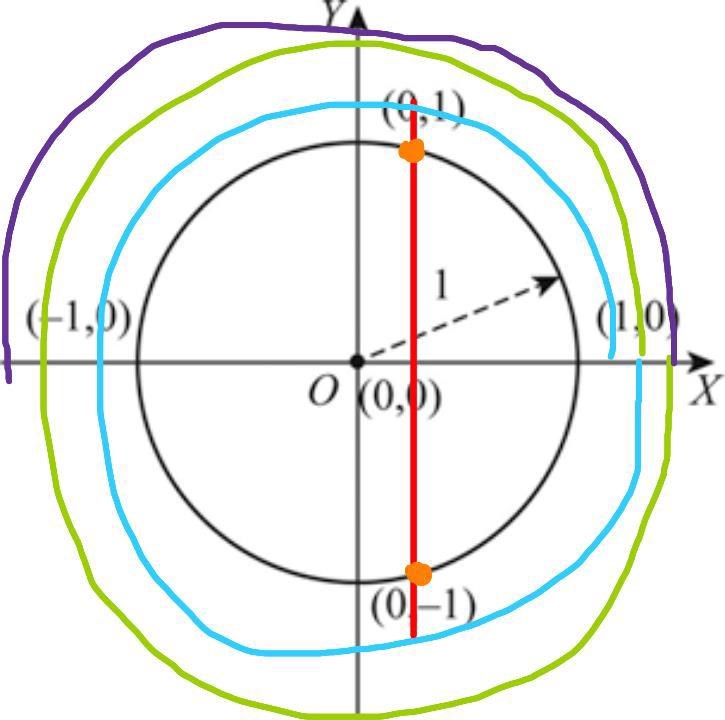
Cheezus på nåt anledning trodde jag att det var också:

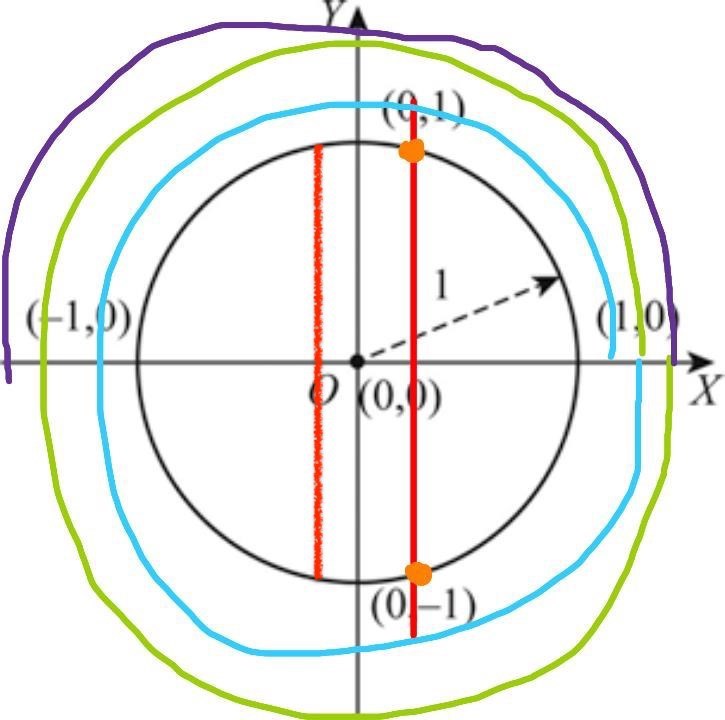
Men eftersom cos(x)=0.25, var det bara dem positiva lösningar som gällde va?

Precis.

Allt det känns fel, vi glömmer det tillsammans med mitt rykte!

Svara

Visa senaste svar