Dynamik; Bestämma hastighet

Jag ska räkna ut hastigheten i punkten B i läge 2. Enligt följande problemformulering:

"Två smala homogena stänger, vardera med massan m och längden L, är sammankopplade med en friktionsfri sprint vid A. Stången OA är ledlagrad vid O. Stödet vid B tillåter vertikal rörelse hos ändpunkten för stång AB. Konstruktionen släpps från vila i läge [1]. Försumma friktionen och bestäm farten för punkten B i läge [2]. (m, L och g är givna storheter)"

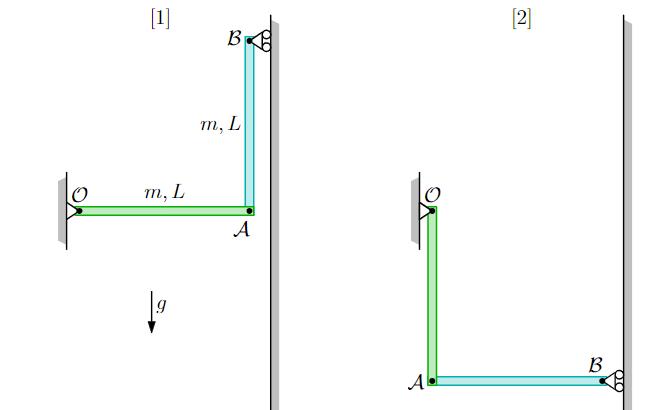
Eftersom det är 2 lägen tänker jag att man kan använda mekaniska energisatsen.

Jag använder: ochi Med V_e=0. Jag tänker då att jag får ta K och V_g för båda stängerna så att det blir $V_{g 1} = m g y_{O A 1} + m g y_{A B 1}$ , $V_{g 2} = m g y_{O A 2} + m g y_{A B 2}$ , $K_{1} = \frac{1}{2} m {v_{G, O A 1}}^{2} + \frac{1}{2} I_{G} {ω^{2}}_{O A 1} + \frac{1}{2} m {v_{G, A B 1}}^{2} + \frac{1}{2} I_{G} {ω^{2}}_{A B 1}$ och $K_{2} = \frac{1}{2} m {v_{G, O A 2}}^{2} + \frac{1}{2} I_{G} {ω^{2}}_{O A 2} + \frac{1}{2} m {v_{G, A B 2}}^{2} + \frac{1}{2} I_{G} {ω^{2}}_{A B 2}$ . Ska man tänka såhär?

Ja, energin för systemet är bevarad. Men stängerna släpps från vila, vad innebär det för de ursprungliga vinkelhastigheterna?

Du kan också finna kinematiska samband mellan de linjära hastigheterna och vinkelhastigheterna i det nedre läget.

Tänk på att det är skillnad mellan att rotera en stång kring dess ändpunkt och att rotera en stång kring dess tyngdpunktscentrum.

D4NIEL skrev:
Ja, energin för systemet är bevarad. Men stängerna släpps från vila, vad innebär det för de ursprungliga vinkelhastigheterna?

Du kan också finna kinematiska samband mellan de linjära hastigheterna och vinkelhastigheterna i det nedre läget.

Tänk på att det är skillnad mellan att rotera en stång kring dess ändpunkt och att rotera en stång kring dess tyngdpunktscentrum.

De ursprungliga vinkelhastigheterna borde vara noll om det släpps från vila (för $v = 0 \Rightarrow ω = 0$ , right?), så $K_{1} = 0$ .

Så jag behöver alltså ta fram $v_{G}$ samt $ω$ för de båda stängerna

Vill du utveckla lite vad du menar är skillnaden om var man roterar stången? :)

För i lösningsförslaget har dom räknat ut hastigheten för hela stången och sedan använt momentancentrum för att få fram $v_{G}$ , då förstår jag inte riktigt hur man tänker när man gör så

jonte12 skrev:
Så jag behöver alltså ta fram $v_{G}$ samt $ω$ för de båda stängerna

Vill du utveckla lite vad du menar är skillnaden om var man roterar stången? :)

För i lösningsförslaget har dom räknat ut hastigheten för hela stången och sedan använt momentancentrum för att få fram $v_{G}$ , då förstår jag inte riktigt hur man tänker när man gör så

Det är en bra början att ta fram kinematiska samband för tyngdpunkternas rörelser och hur de relaterar till vinkelhastigheterna.

Med skillnaden mellan rotationsaxlarna menar jag bara att runt tyngdpunktsscentrum är

$I_G=\frac{1}{12}mL^2$

Men runt änpdpunkten t.ex. OA

$I_A=\frac{1}{3}mL^2$

Visa ditt försök så kan vi säkert klura ut om eller var det blir fel. Och börja som sagt gärna med de kinematiska sambanden så blir det enklare.

Svara

Visa senaste svar