Linjär Algebra: Egenvärden med skalär framför matris (Matematik/Universitet)

Ett bra sätt att tänka på detta är att fundera på vad egenvärden betyder/motsvarar, rent geometriskt. Om en matris har egenvärde 3, med tillhörande egenvektor [3, 1], vad betyder det? :)

Som jag förstått det: Att egenvektorn (3, 1) avbildas och har samma riktning men 3ggr så lång.

Bingo! Om vi då har en matris som gör någon viss förändring av alla vektorer, och sedan krymper dem med en faktor 1/13, vad händer då med egenvärdena? :)

De blir såklart också krympta med en faktor 1/13!
Tack!

Har du kanske lust att ge mig något tips på b) också?

Bingo! Kom ihåg det gamla djungelordspråket:

I linjär algebra, when in doubt, gå tillbaka till den geometriska tolkningen.

😉

Då ska vi se, här skulle jag nog rita. Vad händer med enhetsvektorerna när de utsätts för A? :)

Om det är en spegling, vad kan du säga om egenvärden och egenvektorer?

Om det är en projektion, vad kan du säga om egenvärden och egenvektorer?

Om det är en rotation, vad kan du säga om egenvärden och egenvektorer?

Ae₁=1/13 * (-5, 12)

Ae₂= 1/13 * (12, 5)

Skulle det räcka att redan här säga att det är en rotation eftersom att båda enhetsvektorernas avbildningar är ortogonala?

Du behöver undersöka om det skett en spegling också. Dessutom har det ju skett en förändring av vektorernas storlek. :)

Nej, det är fel. En rotation vrider ju varje vektor med någon given vinkel v. Om v $\neq$ n $π$ , så betyder det att x och Ax inte kan vara parallella, så det kan inte finnas några (reella) egenvärden och egenvektorer. Om v = n $π$ så är A antingen I eller -I. Om A = I så är 1 det enda egenvärdet och alla (nollskilda) vektorer är egenvektorer. Om A = -I så är -1 det enda egenvärdet och alla (nollskilda) vektorer är egenvektorer.

Aa nu ser jag varför jag självklart inte kan dra slutsatsen att det är rotation..

Jag är dock fortfarande lite förvirrad, har aldrig tidigare sett någon uppgift där jag behövt tolka en matris och se vilken slags avbildning det är. Finns det något systematiskt sätt att göra det på?

Facit säger såhär men jag hänger inte med alls vad som gjordes: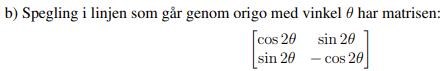

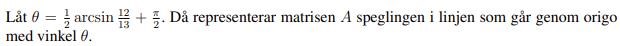
Du kan se en spegling S av en vektor x i en linje genom origo som följande process.

Dela upp vektorn i komposanter u och v, där u är parallell med linjen och v är vinkelrät mot linjen.

Den speglade vektorn Sx är då lika med u - v.

Om du har en vektor x som är parallell med linjen så får du att Sx = x, dvs egenvektor med egenvärde 1.

Om du har en vektor x som är vinkelrät mot linjen så får du Sx = -x, dvs en egenvektor med egenvärde -1.

Om du har en vektor x som varken är parallell med eller vinkelrät mot linjen så är vektorn ingen egenvektor till S. Visa detta!

Så speglingen S har egenvärden 1 och -1 och egenvektorer svarande mot olika egenvärden är ortogonala.

Omvänt, om du har en 2x2 matris A med egenvärden 1 och -1 där egenvektorer svarande mot olika egenvärden är ortogonala så representerar matrisen A en spegling i en linje genom origo. Visa detta!

Att räkna med olika metoder är såklart bra, men jag har funnit att (särskilt i två dimensioner) den överlägset enklaste metoden för att tolka en transformation är att rita upp ett koordinatsystem med enhetsvektorer, och sedan rita ut $T (e_{1})$ och $T (e_{2})$ . Då syns det oftast väldigt tydligt vilken sorts transformation som T är. :)

Det kan hända att ni fått lära er en sats vars innebörd är

Om $A$ är en ortogonal $2x2$ -matris är avbildningen $y=Ax$ på $\mathbb{R}^2$ en geometrisk rotation om $\det\,A=1$ , annars en spegling i den linje som delar vinkeln mellan $A\mathbf{e}_1$ och $\mathbf{e}_1$ mitt itu.

I det här fallet har vi en ortogonal matris med $\det\,A=-1$ , alltså en spegling i linjen genom origo med vinkeln som ges av halva vinkeln mellan $A\mathbf{e}_1$ och x-axeln.

Vi noterar också att facit har krånglat till det för sig. Vinkeln ska vara $\theta=\frac{\pi}{2}-\frac{1}{2}\arcsin(\frac{12}{13})$